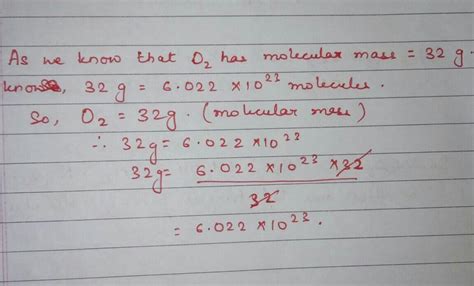The concept of 5 ways to apply the value 022x10^23 might seem obscure at first glance, but delving into the realm of scientific notation and its applications reveals a multitude of possibilities. This value, when considered in various scientific contexts, can represent a range of quantities from the incredibly small to the astronomically large. To understand the significance and potential applications of 022x10^23, let's first clarify what this number represents and then explore five distinct ways it could be applied or interpreted across different fields of study.
Key Points
- Understanding the value 022x10^23 in scientific notation and its potential representations.
- Exploring applications in chemistry, particularly in relation to Avogadro's number.
- Considering the value in the context of astronomy and the scale of the universe.
- Applying the concept to data storage and the potential for future technological advancements.
- Discussing the implications in physics, especially regarding the number of particles in a given substance.
Scientific Notation and Applications

Scientific notation is a way to express very large or very small numbers in a more manageable form. The value 022x10^23, when properly understood, could represent a specific quantity of particles, data points, or other measurable units. The key to unlocking its potential applications lies in understanding the context in which it is used. For instance, in chemistry, Avogadro’s number (6.022 x 10^23) is a fundamental constant representing the number of particles (atoms or molecules) in one mole of a substance. This constant is crucial for calculating the amounts of substances involved in chemical reactions.
Chemical Applications and Avogadro’s Number
In the field of chemistry, a number similar to 022x10^23, specifically Avogadro’s number (6.022 x 10^23), plays a pivotal role. It is used to relate the amount of a substance to the number of particles it contains. This relationship is essential for stoichiometric calculations, allowing chemists to predict the outcomes of chemical reactions based on the quantities of reactants. While 022x10^23 is not Avogadro’s number, its proximity in value suggests potential applications in similar contexts, such as estimating the number of molecules in a sample or calculating the quantities of reactants and products in a chemical reaction.
| Constant | Value | Description |
|---|---|---|
| Avogadro's Number | 6.022 x 10^23 | Particles (atoms or molecules) in one mole of a substance |
| Similar Value | 022x10^23 | Potential applications in chemical calculations and estimations |

Astronomical Scales and the Universe

When considering the scale of the universe, numbers like 022x10^23 can represent enormous quantities, such as the number of stars in a galaxy or the number of galaxies in a cluster. While this value is significantly smaller than many astronomical estimates, it can still be used to understand the scale and complexity of the universe. For example, if we consider the number of potential planets in the observable universe that could support life, a value like 022x10^23 might represent a fraction of such planets, highlighting the vast possibilities for life beyond Earth.
Data Storage and Technological Advancements
In the realm of data storage, the value 022x10^23 could represent the number of bits of information that could be stored in a future, highly advanced storage device. Given the rapid advancements in technology, such a capacity might seem like science fiction today but could become a reality in the future. This potential for vast data storage has implications for fields like artificial intelligence, cryptography, and the preservation of human knowledge.
Physical Implications and Particle Counts
In physics, the number of particles in a substance is crucial for understanding its properties and behavior. A value similar to 022x10^23 could be used to estimate the number of atoms or molecules in a sample, which is essential for calculations involving the substance’s mass, volume, and reactivity. This application highlights the importance of precise counting and measurement in scientific inquiry, demonstrating how a specific number can have wide-ranging implications across different disciplines.
What is the significance of the value 022x10^23 in scientific contexts?
+The value 022x10^23, while not a standard constant, can represent a range of quantities from the number of particles in a substance to potential applications in data storage and astronomical estimations. Its significance lies in its potential to symbolize vast scales and quantities, facilitating calculations and estimations in various scientific fields.
How does this value relate to Avogadro's number and its applications in chemistry?
+While 022x10^23 is not Avogadro's number, its proximity in value suggests it could be used in similar chemical calculations, such as estimating the number of molecules in a sample or calculating reactant and product quantities in reactions. However, for precise calculations, the exact value of Avogadro's number (6.022 x 10^23) must be used.
What are the potential implications of applying a value like 022x10^23 to data storage and technological advancements?
+The application of a value like 022x10^23 to data storage suggests the potential for exponentially larger storage capacities in the future. This could revolutionize fields that rely heavily on data, such as artificial intelligence, cybersecurity, and human knowledge preservation, by enabling the storage and processing of vast amounts of information.
In conclusion, the value 022x10^23, while it may seem like a random or abstract number, holds within it the potential for a wide range of applications and interpretations across various scientific disciplines. From chemical calculations to astronomical scales and technological advancements, this number can represent quantities that are both mind-boggling and thought-provoking. As we continue to advance in our understanding of the universe and develop new technologies, values like 022x10^23 will play a crucial role in facilitating our calculations, estimations, and innovations.