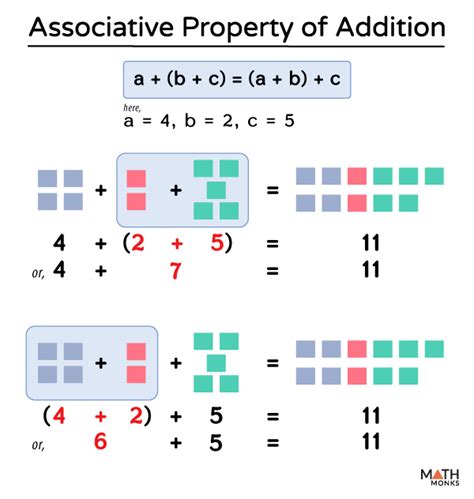
The associative property of addition is a fundamental concept in mathematics that describes how numbers can be grouped when adding them together. This property is essential in various mathematical operations, including simple arithmetic, algebra, and even advanced mathematical theories. Understanding the associative property of addition is crucial for anyone looking to grasp the basics of mathematics and apply them in real-world problems.
Definition and Explanation

The associative property of addition states that when adding three or more numbers together, the order in which the numbers are grouped does not change the result. This can be expressed as (a + b) + c = a + (b + c), where a, b, and c are the numbers being added. The property implies that the way we pair the numbers does not affect the final sum, as long as the order of the numbers remains the same.
For instance, consider the expression 2 + 3 + 4. According to the associative property, we can group the numbers in different ways without changing the result. So, (2 + 3) + 4 = 2 + (3 + 4) = 9. This demonstrates that the associative property holds true for addition, allowing us to add numbers in any order we choose, as long as we maintain the same grouping.
Examples and Applications
To further illustrate the associative property of addition, let’s consider a few more examples. Suppose we want to calculate the sum of 5 + 6 + 7. Using the associative property, we can group the numbers as (5 + 6) + 7 or 5 + (6 + 7). In both cases, the result is the same: 18. This property makes it easier to perform mental calculations and simplify complex expressions.The associative property of addition has numerous applications in mathematics and real-world problems. For instance, in algebra, it is used to simplify expressions and solve equations. In geometry, it is applied to calculate the perimeter and area of shapes. Even in everyday life, we use the associative property when calculating the total cost of items or the distance traveled.
| Expression | Grouping | Result |
|---|---|---|
| 2 + 3 + 4 | (2 + 3) + 4 | 9 |
| 2 + 3 + 4 | 2 + (3 + 4) | 9 |
| 5 + 6 + 7 | (5 + 6) + 7 | 18 |
| 5 + 6 + 7 | 5 + (6 + 7) | 18 |

Key Points
- The associative property of addition states that the order in which numbers are grouped does not change the result.
- The property can be expressed as (a + b) + c = a + (b + c), where a, b, and c are the numbers being added.
- The associative property has numerous applications in mathematics and real-world problems, including algebra, geometry, and everyday calculations.
- Understanding the associative property of addition is essential for simplifying complex expressions and performing mental calculations.
- The property demonstrates the flexibility of mathematical operations and allows us to add numbers in any order we choose, as long as we maintain the same grouping.
Implications and Extensions

The associative property of addition has significant implications for various mathematical operations. For instance, it allows us to extend the property to more complex expressions, such as (a + b) + (c + d) = a + (b + (c + d)). This extension enables us to simplify complex expressions and perform calculations with ease.
Furthermore, the associative property of addition is closely related to other mathematical properties, such as the commutative and distributive properties. The commutative property of addition states that the order of the numbers being added does not change the result, i.e., a + b = b + a. The distributive property, on the other hand, states that multiplication can be distributed over addition, i.e., a(b + c) = ab + ac.
By understanding the associative property of addition and its relationships with other mathematical properties, we can develop a deeper appreciation for the structure and beauty of mathematics. This knowledge can also be applied to various real-world problems, such as calculating the cost of goods, measuring the distance between objects, and optimizing mathematical models.
Historical Context and Evolution
The associative property of addition has its roots in ancient mathematics, where it was used to perform calculations and solve problems. The property was first formally stated by the ancient Greek mathematician Euclid, who recognized its importance in simplifying complex expressions.Over time, the associative property of addition has evolved to become a fundamental concept in mathematics, with applications in various fields, including algebra, geometry, and calculus. The property has been extensively used by mathematicians and scientists, such as Isaac Newton and Albert Einstein, to develop new mathematical theories and models.
Today, the associative property of addition remains a crucial concept in mathematics, with ongoing research and applications in fields such as computer science, physics, and engineering. By understanding the history and evolution of this property, we can appreciate the contributions of mathematicians and scientists who have shaped our understanding of mathematics and its applications.
What is the associative property of addition?
+The associative property of addition states that the order in which numbers are grouped does not change the result, i.e., (a + b) + c = a + (b + c).
What are the applications of the associative property of addition?
+The associative property of addition has numerous applications in mathematics and real-world problems, including algebra, geometry, and everyday calculations.
How is the associative property of addition related to other mathematical properties?
+The associative property of addition is closely related to other mathematical properties, such as the commutative and distributive properties, and is used to simplify complex expressions and perform calculations.
In conclusion, the associative property of addition is a fundamental concept in mathematics that demonstrates the flexibility of mathematical operations. By understanding this property, we can simplify complex expressions, perform mental calculations, and apply mathematical concepts to real-world problems. The property has significant implications for various mathematical operations and is closely related to other mathematical properties, such as the commutative and distributive properties. As we continue to explore and apply mathematical concepts, the associative property of addition remains a crucial concept that underlies many mathematical theories and models.