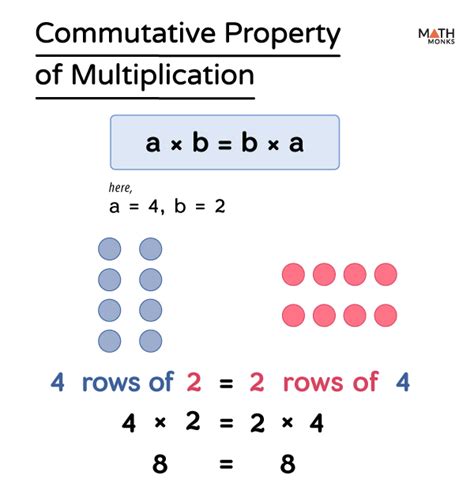
The commutative property of multiplication is a fundamental concept in mathematics that states that the order of the factors does not change the product. In other words, when we multiply two numbers, the result is the same regardless of the order in which we multiply them. This property is often represented mathematically as $a \times b = b \times a$, where $a$ and $b$ are any real numbers. Understanding this concept is crucial for building a strong foundation in mathematics, as it is used extensively in various mathematical operations, including algebra, geometry, and calculus.
Key Points
- The commutative property of multiplication states that the order of the factors does not change the product.
- This property is represented mathematically as $a \times b = b \times a$.
- Understanding the commutative property is essential for building a strong foundation in mathematics.
- The commutative property is used extensively in various mathematical operations, including algebra, geometry, and calculus.
- Mastering this concept can help simplify complex mathematical problems and improve problem-solving skills.
Understanding the Commutative Property
To illustrate the commutative property of multiplication, consider the example of 3 \times 4. According to the commutative property, we can rewrite this expression as 4 \times 3, and the result will be the same. In fact, 3 \times 4 = 12 and 4 \times 3 = 12, demonstrating that the order of the factors does not affect the product. This property holds true for all real numbers, including integers, fractions, and decimals.
Examples and Applications
The commutative property of multiplication has numerous applications in mathematics and real-world problems. For instance, in algebra, we can use this property to simplify expressions and equations. Consider the expression 2x \times 3y, where x and y are variables. Using the commutative property, we can rewrite this expression as 3y \times 2x, which can be further simplified to 6xy. This property is also essential in geometry, where we need to calculate the area and perimeter of shapes. For example, the area of a rectangle is given by the formula A = l \times w, where l is the length and w is the width. According to the commutative property, we can rewrite this formula as A = w \times l, and the result will be the same.
| Mathematical Operation | Example | Result |
|---|---|---|
| Multiplication | $3 \times 4$ | $12$ |
| Multiplication | $4 \times 3$ | $12$ |
| Algebraic Expression | $2x \times 3y$ | $6xy$ |
| Geometric Formula | $A = l \times w$ | $A = w \times l$ |

Real-World Applications

The commutative property of multiplication has numerous real-world applications, including science, engineering, and finance. In science, this property is used to calculate the area and volume of objects, as well as the force and pressure exerted on an object. In engineering, the commutative property is used to design and build structures, such as bridges and buildings. In finance, this property is used to calculate interest rates and investment returns. For example, when calculating the interest on a loan, we can use the formula I = P \times r \times t, where I is the interest, P is the principal amount, r is the interest rate, and t is the time period. According to the commutative property, we can rewrite this formula as I = r \times t \times P, and the result will be the same.
Conclusion and Future Directions
In conclusion, the commutative property of multiplication is a fundamental concept in mathematics that has numerous applications in various fields. By understanding and applying this property, students can develop a deeper understanding of mathematical concepts and improve their problem-solving skills. As mathematics continues to evolve and play an increasingly important role in our daily lives, it is essential to master this concept and explore its applications in different contexts. Future research directions may include exploring the commutative property in other mathematical operations, such as addition and division, and developing new applications in fields like artificial intelligence and data science.
What is the commutative property of multiplication?
+The commutative property of multiplication states that the order of the factors does not change the product. This property is represented mathematically as a \times b = b \times a.
What are the applications of the commutative property of multiplication?
+The commutative property of multiplication has numerous applications in mathematics, science, engineering, and finance. It is used to simplify expressions and equations, calculate the area and volume of objects, and design and build structures.
How can I master the commutative property of multiplication?
+To master the commutative property of multiplication, practice applying it to different mathematical operations and real-world problems. Start with simple examples and gradually move on to more complex problems. You can also use online resources and educational videos to supplement your learning.