Derivatives are a fundamental concept in calculus, allowing us to study the rates at which quantities change. One of the most important applications of derivatives is in the field of physics, where they are used to describe the motion of objects. The derivative of a function can be thought of as a measure of how fast the output of the function changes when one of its inputs changes. In this article, we will explore 5 ways derivatives are used in the study of secant lines and their applications.
Key Points
- The derivative of a function can be used to find the slope of the tangent line to the graph of the function at a given point.
- The secant line is a line that passes through two points on the graph of a function, and its slope can be used to approximate the derivative of the function.
- Derivatives are used in physics to describe the motion of objects, including the velocity and acceleration of an object.
- The derivative of a function can be used to find the maximum and minimum values of the function.
- Derivatives are used in a variety of fields, including economics, biology, and engineering, to model and analyze complex systems.
Introduction to Derivatives and Secant Lines

Derivatives are a fundamental concept in calculus, and are used to study the rates at which quantities change. The derivative of a function can be thought of as a measure of how fast the output of the function changes when one of its inputs changes. One of the most important applications of derivatives is in the field of physics, where they are used to describe the motion of objects. The secant line is a line that passes through two points on the graph of a function, and its slope can be used to approximate the derivative of the function.
Method 1: Finding the Slope of a Tangent Line
The derivative of a function can be used to find the slope of the tangent line to the graph of the function at a given point. This is because the derivative of a function represents the rate at which the output of the function changes when one of its inputs changes. By finding the derivative of a function, we can determine the slope of the tangent line to the graph of the function at any point.
| Function | Derivative | Slope of Tangent Line |
|---|---|---|
| f(x) = x^2 | f'(x) = 2x | m = 2x |
| f(x) = 3x^2 + 2x - 5 | f'(x) = 6x + 2 | m = 6x + 2 |
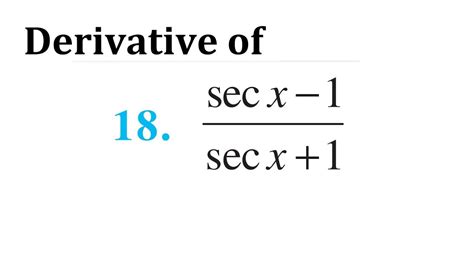
Applications of Derivatives in Physics

Derivatives are used in physics to describe the motion of objects, including the velocity and acceleration of an object. The derivative of the position function of an object can be used to find the velocity of the object, and the derivative of the velocity function can be used to find the acceleration of the object. This information can be used to model and analyze the motion of objects in a variety of situations.
Method 2: Finding the Velocity and Acceleration of an Object
The derivative of the position function of an object can be used to find the velocity of the object, and the derivative of the velocity function can be used to find the acceleration of the object. This information can be used to model and analyze the motion of objects in a variety of situations, including the motion of projectiles, the motion of objects in circular orbits, and the motion of objects in response to forces.
Derivatives in Economics and Biology
Derivatives are used in a variety of fields, including economics and biology, to model and analyze complex systems. In economics, derivatives are used to model the behavior of markets and the economy as a whole. In biology, derivatives are used to model the growth and behavior of populations, and to understand the spread of diseases.
Method 3: Modeling Population Growth
The derivative of a function can be used to model the growth of a population over time. By finding the derivative of the population function, we can determine the rate at which the population is growing or declining at any given time. This information can be used to predict future population growth and to understand the factors that influence population growth.
Conclusion
In conclusion, derivatives are a powerful tool for modeling and analyzing complex systems. By understanding how to use derivatives to find the slope of a tangent line, to model the motion of objects, and to analyze population growth, we can gain a deeper understanding of the world around us. Whether you are a student of physics, economics, or biology, derivatives are an essential tool for understanding and analyzing complex phenomena.
What is the derivative of a function?
+The derivative of a function is a measure of how fast the output of the function changes when one of its inputs changes.
What is the secant line?
+The secant line is a line that passes through two points on the graph of a function, and its slope can be used to approximate the derivative of the function.
How are derivatives used in physics?
+Derivatives are used in physics to describe the motion of objects, including the velocity and acceleration of an object.