Derivative of Tan x Formula

The derivative of the tangent function, denoted as $\frac{d}{dx} \tan x$, is a fundamental concept in calculus, particularly in the realm of trigonometry. To understand the derivative of $\tan x$, it's essential to start with the basic definition of the tangent function: $\tan x = \frac{\sin x}{\cos x}$. This definition forms the basis of deriving the derivative of $\tan x$.

Derivation of the Derivative of Tan x

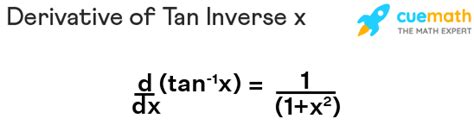
The process of finding the derivative of \tan x involves applying the quotient rule of differentiation. The quotient rule states that if we have a function of the form f(x) = \frac{g(x)}{h(x)}, then its derivative f'(x) is given by the formula: f'(x) = \frac{h(x)g'(x) - g(x)h'(x)}{(h(x))^2}. Applying this rule to \tan x = \frac{\sin x}{\cos x}, we can find its derivative.

Applying the Quotient Rule

To find the derivative of \tan x using the quotient rule, we first identify g(x) = \sin x and h(x) = \cos x. Then, we find their derivatives: g'(x) = \cos x and h'(x) = -\sin x. Plugging these into the quotient rule formula gives us: \frac{d}{dx} \tan x = \frac{\cos x \cdot \cos x - \sin x \cdot (-\sin x)}{(\cos x)^2}. Simplifying this expression yields: \frac{\cos^2 x + \sin^2 x}{\cos^2 x}. Since \cos^2 x + \sin^2 x = 1 (by the Pythagorean identity), the derivative simplifies further to: \frac{1}{\cos^2 x}.

Recognizing that $\frac{1}{\cos^2 x}$ is equivalent to $\sec^2 x$ (since $\sec x = \frac{1}{\cos x}$), we conclude that the derivative of $\tan x$ is $\sec^2 x$. This result is a cornerstone in trigonometric calculus and has numerous applications in physics, engineering, and other fields where trigonometric functions are used to model periodic phenomena.

Applications and Interpretations

The derivative of \tan x has practical implications in fields such as physics and engineering, where it is used to model the motion of objects along curved paths or to analyze the behavior of electrical circuits. For instance, in the study of simple harmonic motion, understanding how the tangent function and its derivative relate to the position, velocity, and acceleration of an object is crucial. Moreover, the derivative of \tan x appears in the analysis of AC circuits, where the impedance of a circuit can be represented using trigonometric functions.

Technical Specifications and Calculus

In a more mathematical context, the derivative of \tan x plays a role in advanced calculus topics, such as the study of differential equations and integral calculus. The ability to differentiate \tan x and other trigonometric functions is essential for solving differential equations that model real-world phenomena, such as population growth, chemical reactions, and electrical circuits. Furthermore, understanding the derivatives of trigonometric functions is critical in the application of integration techniques, such as substitution and integration by parts, which are used to find the antiderivatives of complex functions.

In conclusion, the derivative of $\tan x$ is a pivotal concept in calculus, offering insights into the behavior of trigonometric functions and their applications in modeling real-world phenomena. The process of deriving $\frac{d}{dx} \tan x$ and understanding its implications not only deepens one's grasp of mathematical principles but also fosters a nuanced appreciation for the intricate relationships between functions and their derivatives.