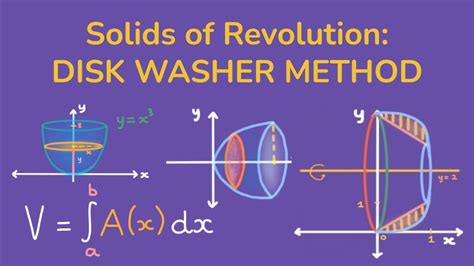The disk and washer method, also known as the disk method or ring method, is a technique used in calculus to calculate the volume of a solid of revolution. This method is employed when a region bounded by a curve is rotated about a horizontal or vertical axis, generating a solid. The disk and washer method is a fundamental concept in integral calculus, allowing us to find the volumes of complex shapes that would be difficult to calculate using other methods.
To understand the disk and washer method, it's essential to have a basic knowledge of calculus, particularly integration. The method involves dividing the region into infinitesimally thin disks or washers and then integrating the areas of these disks or washers with respect to the axis of rotation. The choice between the disk method and the washer method depends on the shape of the region and the axis of rotation. If the region is rotated about an axis and does not contain the axis, the disk method is used. However, if the region is rotated about an axis that it contains, and the region has a hole or an empty space, the washer method is applied.
Key Points
- The disk and washer method is used to calculate the volume of a solid of revolution.
- The method involves integrating the areas of infinitesimally thin disks or washers with respect to the axis of rotation.
- The choice between the disk method and the washer method depends on the shape of the region and the axis of rotation.
- The disk method is used when the region does not contain the axis of rotation.
- The washer method is used when the region contains the axis of rotation and has a hole or empty space.
Understanding the Disk Method

The disk method is applied when the region bounded by a curve is rotated about an axis that does not intersect the region. The volume of the solid formed is calculated by integrating the area of the disks with respect to the axis of rotation. The formula for the volume using the disk method is (V = \pi \int{a}^{b} [f(x)]^2 dx) when rotating about the x-axis, where (f(x)) is the function that bounds the region, and (a) and (b) are the limits of integration. For rotation about the y-axis, the formula adjusts to (V = \pi \int{a}^{b} [f(y)]^2 dy), with (f(y)) representing the function in terms of (y).
Applying the Disk Method to Real-World Problems
The disk method has numerous applications in engineering, architecture, and physics, where the volumes of complex shapes need to be accurately calculated. For instance, in the design of water tanks, the volume of the tank can be determined using the disk method if the tank’s shape can be modeled as a solid of revolution. Similarly, in mechanical engineering, the disk method can be used to calculate the volume of components like gears and pulleys, which often have shapes that can be described as solids of revolution.
| Region Characteristics | Disk Method Formula |
|---|---|
| Rotation about x-axis | V = \pi \int_{a}^{b} [f(x)]^2 dx |
| Rotation about y-axis | V = \pi \int_{a}^{b} [f(y)]^2 dy |

Understanding the Washer Method

The washer method is an extension of the disk method and is used when the region being rotated contains a hole or empty space. This method is particularly useful for calculating the volumes of hollow cylinders, tubes, and other shapes with a central cavity. The formula for the volume using the washer method involves subtracting the volume of the inner solid from the volume of the outer solid. For rotation about the x-axis, the formula is (V = \pi \int_{a}^{b} ([f(x)]^2 - [g(x)]^2) dx), where (f(x)) is the outer radius and (g(x)) is the inner radius of the washer.
Applying the Washer Method to Complex Shapes
The washer method is invaluable for calculating the volumes of complex, hollow shapes. In construction, for example, it can be used to determine the volume of concrete needed for a hollow column. In aerospace engineering, the method can help calculate the volume of fuel tanks that have complex, hollow geometries. The key to applying the washer method successfully is to accurately define the outer and inner boundaries of the shape and to select the appropriate limits of integration.
The washer method, like the disk method, relies on the principle of integrating the area of infinitesimally thin washers with respect to the axis of rotation. However, because it accounts for the removal of material (the hole or empty space), it provides a more versatile tool for volume calculations of a wide range of solids of revolution.
What is the primary difference between the disk and washer methods?
+The primary difference is that the disk method is used for solid regions without holes, while the washer method is used for regions that contain a hole or empty space, requiring the subtraction of the inner volume from the outer volume.
How do you choose between rotating about the x-axis or y-axis?
+The choice depends on the orientation of the region and the axis of rotation. If the region's boundary functions are more easily expressed in terms of x, rotation about the x-axis is chosen. If the functions are more easily expressed in terms of y, rotation about the y-axis is chosen.
What are some common applications of the disk and washer methods?
+These methods are commonly applied in engineering and architecture to calculate volumes of complex shapes, such as water tanks, mechanical components, and building structures. They are also used in physics to model real-world phenomena, such as the volume of celestial bodies.
In conclusion, the disk and washer methods are powerful tools in calculus for calculating the volumes of solids of revolution. By understanding the principles behind these methods and how to apply them, one can solve a wide range of problems in mathematics, physics, engineering, and other fields. The key to mastering these methods is practice and a deep understanding of the underlying calculus concepts.