When dealing with rational functions, one of the critical aspects to analyze is the presence of vertical asymptotes. These occur where the denominator of the function equals zero, causing the function to become undefined. The process of finding vertical asymptotes is straightforward and involves a few key steps. In this article, we will delve into the method of identifying vertical asymptotes with ease, exploring the underlying concepts and providing illustrative examples to solidify understanding.
Key Points
- Understanding the concept of vertical asymptotes and their relation to rational functions.
- Learning the steps to find vertical asymptotes, including factoring the denominator and identifying zeros.
- Recognizing the importance of canceling common factors between the numerator and denominator.
- Applying the method to various examples to reinforce comprehension.
- Exploring special cases, such as holes and vertical asymptotes at the same point.
Understanding Vertical Asymptotes
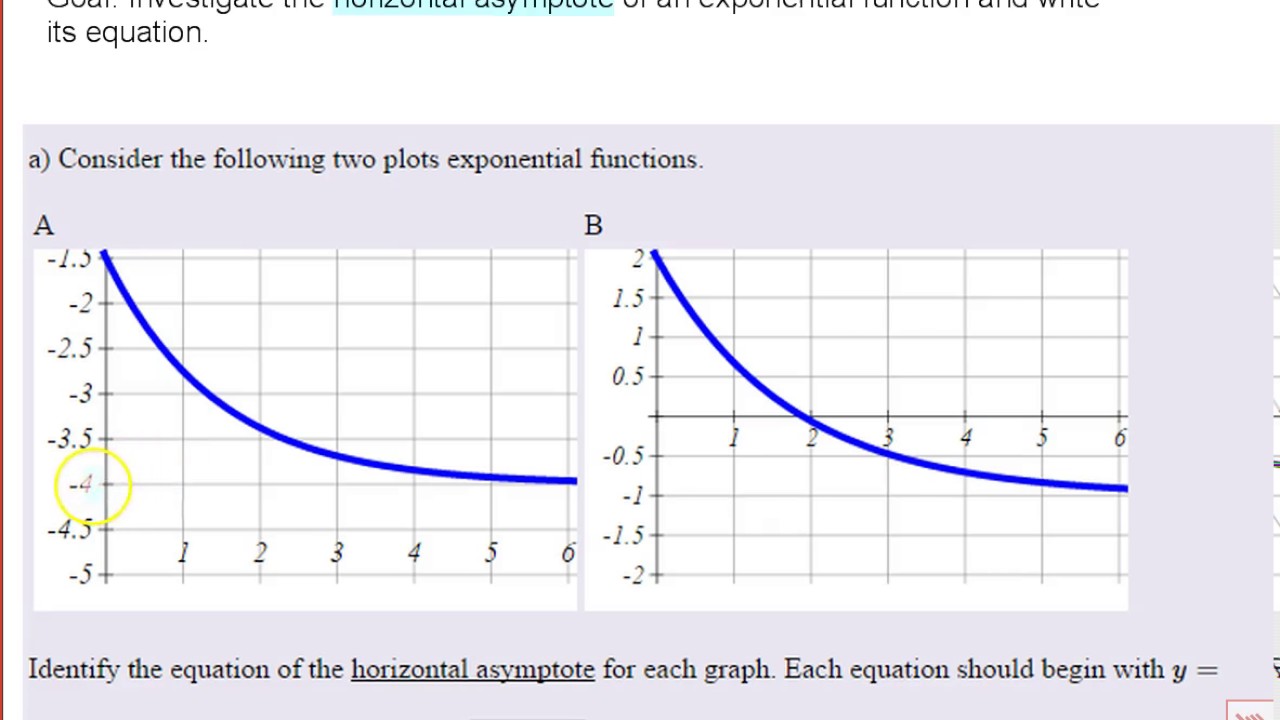
A vertical asymptote is a vertical line that a function approaches but never touches. For rational functions of the form f(x) = \frac{p(x)}{q(x)}, where p(x) and q(x) are polynomials, vertical asymptotes occur at values of x where the denominator, q(x), equals zero, provided that there are no common factors between p(x) and q(x) that would cancel out these zeros.
Steps to Find Vertical Asymptotes
The process of finding vertical asymptotes involves the following steps:
- Factor the denominator to identify its roots. This can be done through various factoring techniques, such as finding the greatest common factor, factoring by grouping, or using the quadratic formula for quadratic expressions.
- Identify the zeros of the denominator. These are the values of x that make the denominator equal to zero.
- Check for common factors between the numerator and the denominator. If there are any, and they cancel out a factor that contributes to a zero in the denominator, then there is a hole at that point rather than a vertical asymptote.
| Function | Denominator Zeros | Vertical Asymptotes |
|---|---|---|
| $f(x) = \frac{1}{x-2}$ | $x = 2$ | $x = 2$ |
| $f(x) = \frac{x-1}{(x-1)(x+3)}$ | $x = 1, x = -3$ | $x = -3$ (since $x = 1$ is a hole) |
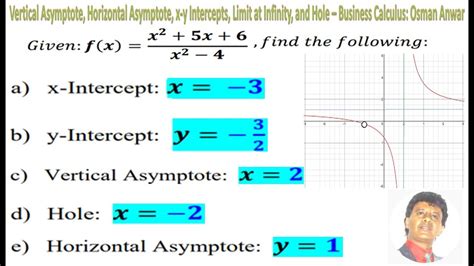
Applying the Method to Examples

To solidify understanding, let’s apply the steps to find vertical asymptotes to several examples:
Example 1: Simple Rational Function
Consider the function f(x) = \frac{1}{x}. The denominator is simply x, which equals zero when x = 0. Since there are no common factors between the numerator and the denominator, x = 0 is a vertical asymptote.
Example 2: Factoring the Denominator
For the function f(x) = \frac{x+1}{x^2 - 4}, we factor the denominator to get f(x) = \frac{x+1}{(x+2)(x-2)}. The zeros of the denominator are x = -2 and x = 2, and since there are no common factors with the numerator, both are vertical asymptotes.
Example 3: Considering Common Factors
Given f(x) = \frac{x-1}{(x-1)(x+1)}, we notice that x = 1 is a zero of both the numerator and the denominator. Thus, x = 1 is a hole, not a vertical asymptote. The only vertical asymptote is at x = -1.
Forward-Looking Implications
Understanding vertical asymptotes is not only essential for analyzing rational functions but also has broader implications in calculus, such as in the study of limits and the behavior of functions as they approach certain values. Recognizing where functions become undefined helps in plotting graphs accurately and interpreting the results in real-world applications.
What is the primary condition for a vertical asymptote to occur in a rational function?
+A vertical asymptote occurs at a value of $x$ where the denominator of the rational function equals zero, provided there are no common factors between the numerator and the denominator that cancel out this zero.
How do common factors between the numerator and denominator affect the identification of vertical asymptotes?
+Common factors that cancel out can turn what would be a vertical asymptote into a hole, indicating that the function is defined at that point but has a gap in its graph.
What is the significance of understanding vertical asymptotes in the broader context of mathematics and real-world applications?
+Understanding vertical asymptotes is crucial for accurately analyzing and interpreting the behavior of rational functions, which has implications in various fields such as physics, engineering, and economics, where these functions are used to model real-world phenomena.
In conclusion, finding vertical asymptotes is a systematic process that involves factoring the denominator of a rational function, identifying its zeros, and checking for any common factors with the numerator. By mastering this skill, one can better understand the behavior of rational functions and apply this knowledge in a wide range of mathematical and real-world contexts.



