Determining limits is a fundamental concept in mathematics, particularly in calculus. It involves finding the value that a function approaches as the input or independent variable gets arbitrarily close to a certain point. Limits are crucial in understanding the behavior of functions, and they have numerous applications in various fields, including physics, engineering, and economics. In this article, we will delve into the concept of limits, explore the different types of limits, and discuss how to determine them easily.
Key Points
- Understanding the concept of limits and their importance in calculus
- Types of limits, including one-sided limits and infinite limits
- Techniques for determining limits, such as direct substitution and factoring
- Applications of limits in real-world problems
- Common challenges and mistakes to avoid when working with limits
Understanding Limits
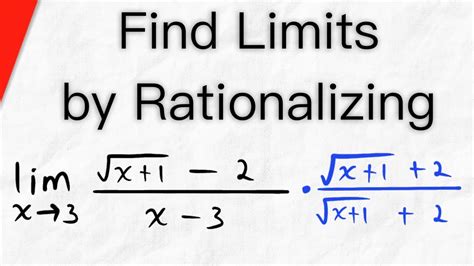
A limit is defined as the value that a function approaches as the input gets arbitrarily close to a certain point. It is denoted by the symbol lim and is often referred to as the limit of the function as x approaches a. For example, the limit of the function f(x) = 2x as x approaches 3 is 6, denoted as lim x→3 2x = 6. Limits can be used to define the basic operations of calculus, such as the derivative and the integral.
Types of Limits
There are several types of limits, including one-sided limits and infinite limits. One-sided limits involve finding the limit of a function as the input approaches a point from one side, either from the left or the right. For example, the limit of the function f(x) = |x| as x approaches 0 from the left is -0, denoted as lim x→0- |x| = -0. Infinite limits involve finding the limit of a function as the input approaches infinity or negative infinity.
| Limit Type | Description |
|---|---|
| One-sided limit | Limit as x approaches a point from one side |
| Infinite limit | Limit as x approaches infinity or negative infinity |
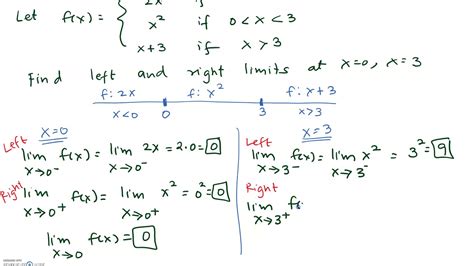
Determining Limits

There are several techniques for determining limits, including direct substitution, factoring, and cancellation. Direct substitution involves substituting the value of x into the function and evaluating the result. Factoring involves factoring the numerator and denominator of a rational function and canceling out common factors. Cancellation involves canceling out common factors in the numerator and denominator of a rational function.
Common Challenges and Mistakes
When working with limits, there are several common challenges and mistakes to avoid. One of the most common mistakes is assuming that a function is continuous at a point without checking. Another mistake is forgetting to consider the properties of the function, such as differentiability and integrability. Additionally, it’s essential to be careful when canceling out common factors in rational functions, as this can lead to incorrect results.
What is the difference between a limit and a function value?
+A limit is the value that a function approaches as the input gets arbitrarily close to a certain point, while a function value is the actual value of the function at a specific point.
How do I determine if a function is continuous at a point?
+A function is continuous at a point if the limit of the function as x approaches the point is equal to the function value at that point.
What is the purpose of limits in calculus?
+Limits are used to define the basic operations of calculus, such as the derivative and the integral, and are essential for understanding the behavior of functions.
In conclusion, determining limits is a crucial concept in calculus, and understanding the different types of limits and techniques for determining them is essential for working with functions. By considering the properties of functions and avoiding common mistakes, you can easily determine limits and apply them to real-world problems. With practice and experience, you can become proficient in determining limits and develop a deeper understanding of calculus and its applications.