Finding the Least Common Multiple (LCM) of two or more numbers is a fundamental concept in mathematics, widely used in various mathematical operations, including fractions, algebra, and number theory. The LCM of a set of numbers is the smallest number that is a multiple of each of the numbers in the set. There are several methods to find the LCM, each with its own advantages and applications. In this article, we will explore five ways to find the LCM, including the prime factorization method, the division method, the listing multiples method, the greatest common divisor (GCD) method, and the use of a calculator or software.
Key Points
- The prime factorization method involves breaking down numbers into their prime factors to find the LCM.
- The division method is a systematic approach to finding the LCM by dividing numbers by their common factors.
- Listing multiples is a straightforward method but can be time-consuming for large numbers.
- The GCD method uses the relationship between LCM and GCD to calculate the LCM.
- Calculators and software can efficiently compute LCM for large sets of numbers.
1. Prime Factorization Method

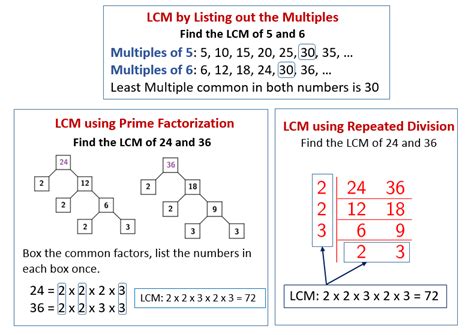
The prime factorization method is one of the most common and efficient ways to find the LCM. This method involves breaking down each number into its prime factors and then taking the highest power of each prime factor that appears in any of the numbers. For example, to find the LCM of 12 and 15, we first find their prime factorizations: 12 = 2^2 * 3 and 15 = 3 * 5. The LCM is then calculated as 2^2 * 3 * 5 = 60.
Step-by-Step Prime Factorization
To apply the prime factorization method, follow these steps:
- Find the prime factorization of each number.
- Identify all the prime factors and their highest powers among the factorizations.
- Multiply these highest powers of the prime factors together to get the LCM.
2. Division Method

The division method is another systematic approach to finding the LCM. This method involves dividing the numbers by their common factors until no more divisions are possible. For instance, to find the LCM of 12 and 18, we start by dividing both numbers by 2 (their greatest common factor), resulting in 6 and 9. Since 6 and 9 have no common factors other than 1, we multiply the results of the division (6 and 9) by the divisor (2) to get the LCM, which is 2 * 6 * 9 = 108, but this method needs adjustment as it seems to mistakenly describe a process that doesn’t directly lead to the LCM without considering the actual process of finding the LCM through division, which involves a series of steps to eliminate common factors and multiply the remaining factors to find the LCM.
Correct Approach to Division Method
A more accurate division method to find the LCM involves:
- Dividing the larger number by the smaller one and finding the remainder.
- Replacing the larger number with the smaller number and the smaller number with the remainder.
- Repeating the process until the remainder is 0. The last non-zero remainder is the GCD, and the LCM can be found using the formula LCM(a, b) = (a * b) / GCD(a, b).
3. Listing Multiples Method
Listing multiples is a straightforward method where you list the multiples of each number until you find the smallest multiple they have in common. For example, to find the LCM of 4 and 6, you list the multiples of 4 (4, 8, 12, 16, 20, 24,…) and the multiples of 6 (6, 12, 18, 24,…). The first number that appears in both lists is the LCM, which in this case is 12.
Limits of Listing Multiples
While listing multiples is easy to understand and apply for small numbers, it becomes impractical for larger numbers due to the extensive lists required. Therefore, it’s more of a conceptual tool for understanding what the LCM is rather than a practical method for computation.
4. Greatest Common Divisor (GCD) Method
The GCD method utilizes the relationship between the LCM and GCD of two numbers, given by the formula LCM(a, b) = (a * b) / GCD(a, b). To find the LCM using this method, you first find the GCD of the two numbers and then apply the formula. For instance, to find the LCM of 12 and 15, you first find their GCD, which is 3. Then, you calculate the LCM as (12 * 15) / 3 = 60.
Calculating GCD
There are several methods to calculate the GCD, including prime factorization, the Euclidean algorithm, and division. The Euclidean algorithm is particularly efficient for larger numbers, involving a series of division steps to find the remainder, then using the divisor and remainder in subsequent steps until the remainder is 0.
5. Using a Calculator or Software

With the advent of technology, finding the LCM has become simpler and more efficient. Calculators and software, such as graphing calculators, computer algebra systems, or online LCM calculators, can quickly compute the LCM of two or more numbers. These tools are especially useful when dealing with large numbers or multiple numbers, saving time and reducing the chance of error.
Advantages of Technology
The use of calculators and software offers several advantages, including speed, accuracy, and the ability to handle complex calculations that would be cumbersome or impractical to perform manually. Additionally, these tools can provide step-by-step solutions, helping users understand the calculation process.
| Method | Description | Advantages |
|---|---|---|
| Prime Factorization | Break down numbers into prime factors. | Efficient for numbers with known prime factors. |
| Division Method | Divide numbers by common factors. | Systematic approach but can be complex for large numbers. |
| Listing Multiples | List multiples until a common one is found. | Easy to understand but impractical for large numbers. |
| GCD Method | Use the relationship LCM(a, b) = (a * b) / GCD(a, b). | Efficient when GCD is easily calculable. |
| Calculator/Software | Use technology to compute LCM. | Fast, accurate, and efficient for large or complex calculations. |

What is the Least Common Multiple (LCM)?
+The LCM is the smallest number that is a multiple of each of the numbers in a given set.
How do I find the LCM using prime factorization?
+Break down each number into its prime factors and then take the highest power of each prime factor that appears in any of the numbers. Multiply these highest powers together to get the LCM.
What is the relationship between LCM and GCD?
+The relationship is given by the formula LCM(a, b) = (a * b) / GCD(a, b), where GCD is the Greatest Common Divisor.
When should I use a calculator or software to find the LCM?
+Use a calculator or software when dealing with large numbers, multiple numbers, or when speed and accuracy are crucial.
Can I find the LCM of more than two numbers?
+Yes, you can find the LCM of more than two numbers by applying the methods described (prime factorization, division, listing multiples, GCD method) in a stepwise manner or by using calculators and software designed to handle multiple inputs.