The concept of periodic functions is fundamental in mathematics, particularly in trigonometry and calculus. A periodic function is a function that repeats its values at regular intervals, known as the period of the function. In this article, we will explore how to find the period of a function easily, using various methods and examples.
Understanding Periodic Functions

A periodic function is defined as a function f(x) that satisfies the condition f(x + T) = f(x) for all x in the domain of the function, where T is a positive constant. The smallest positive value of T for which this condition holds is called the period of the function. Periodic functions are essential in modeling real-world phenomena, such as sound waves, light waves, and population growth.
Types of Periodic Functions
There are several types of periodic functions, including trigonometric functions, exponential functions, and polynomial functions. Trigonometric functions, such as sine and cosine, are the most common examples of periodic functions. These functions have a period of 2π, which means that their values repeat every 2π units.
| Function | Period |
|---|---|
| Sine (sin x) | 2π |
| Cosine (cos x) | 2π |
| Tangent (tan x) | π |

Key Points
- The period of a function is the smallest positive value of T for which f(x + T) = f(x) for all x.
- Trigonometric functions, such as sine and cosine, have a period of 2π.
- Exponential functions and polynomial functions can also be periodic, but their periods depend on their specific forms.
- The period of a function can be found using various methods, including graphical analysis, algebraic manipulation, and numerical computation.
- Understanding the period of a function is crucial in modeling real-world phenomena and solving problems in mathematics and science.
Methods for Finding the Period of a Function

There are several methods for finding the period of a function, including graphical analysis, algebraic manipulation, and numerical computation. Graphical analysis involves plotting the function and observing its repeating pattern. Algebraic manipulation involves using mathematical formulas and equations to derive the period of the function. Numerical computation involves using numerical methods, such as the bisection method or the secant method, to approximate the period of the function.
Graphical Analysis
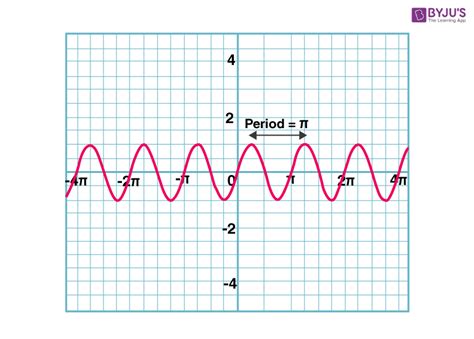
Graphical analysis is a simple and intuitive method for finding the period of a function. By plotting the function, we can observe its repeating pattern and measure the distance between consecutive repetitions. This method is particularly useful for trigonometric functions, such as sine and cosine, which have a characteristic wave-like shape.
For example, consider the function f(x) = sin(x). By plotting this function, we can see that its values repeat every 2π units. Therefore, the period of this function is 2π.
Algebraic Manipulation
Algebraic manipulation is a more rigorous method for finding the period of a function. This method involves using mathematical formulas and equations to derive the period of the function. For example, consider the function f(x) = a sin(bx + c) + d. By using the formula for the period of a sine function, which is T = 2π / |b|, we can derive the period of this function as T = 2π / |b|.
For instance, suppose we have the function f(x) = 2 sin(3x + 1) + 1. Using the formula for the period of a sine function, we can calculate the period of this function as T = 2π / |3| = 2π / 3.
Numerical Computation
Numerical computation is a method for approximating the period of a function using numerical methods. This method is particularly useful for functions that do not have a simple algebraic form or for functions that are difficult to analyze graphically. Numerical computation involves using algorithms, such as the bisection method or the secant method, to approximate the period of the function.
Numerical Example
Suppose we have the function f(x) = x^2 sin(x) + 1. This function does not have a simple algebraic form, and its period is difficult to analyze graphically. Using numerical computation, we can approximate the period of this function as follows:
First, we define the function f(x) = x^2 sin(x) + 1. Then, we use a numerical method, such as the bisection method, to find the roots of the equation f(x + T) - f(x) = 0. The roots of this equation correspond to the period of the function.
Using numerical computation, we can approximate the period of the function f(x) = x^2 sin(x) + 1 as T ≈ 2π.
What is the period of a function?
+The period of a function is the smallest positive value of T for which f(x + T) = f(x) for all x in the domain of the function.
How can we find the period of a function?
+We can find the period of a function using various methods, including graphical analysis, algebraic manipulation, and numerical computation.
What are some common examples of periodic functions?
+Some common examples of periodic functions include trigonometric functions, such as sine and cosine, and exponential functions, such as e^x.
In conclusion, finding the period of a function is a crucial step in understanding and analyzing periodic phenomena. By using various methods, including graphical analysis, algebraic manipulation, and numerical computation, we can determine the period of a function and gain insights into its behavior. Whether we are dealing with trigonometric functions, exponential functions, or other types of periodic functions, understanding the period of a function is essential in modeling real-world phenomena and solving problems in mathematics and science.