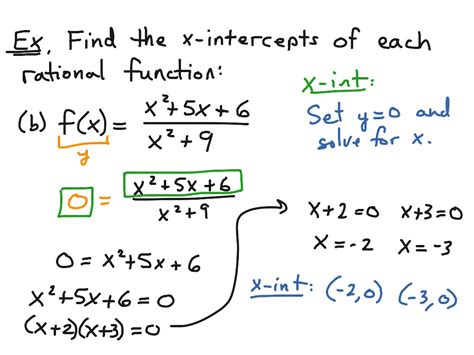
The X intercept of a function is a crucial concept in mathematics, particularly in algebra and graphing. It represents the point at which the function crosses the X-axis, meaning the value of Y is zero. To find the X intercept of a function, we need to set the function equal to zero and solve for X. This process involves understanding the function's equation and applying algebraic techniques to isolate the variable X.
For instance, consider a linear function in the form of f(x) = mx + b, where m is the slope and b is the Y-intercept. To find the X intercept, we set f(x) = 0, resulting in the equation mx + b = 0. Solving for X, we subtract b from both sides and then divide by m, yielding X = -b/m. This calculation gives us the X intercept of the linear function.
In the case of more complex functions, such as quadratic equations (f(x) = ax^2 + bx + c), finding the X intercept involves setting the equation equal to zero and solving for X. This can be achieved through factoring, completing the square, or using the quadratic formula: X = (-b ± √(b^2 - 4ac)) / 2a. Each method has its own applicability depending on the nature of the quadratic equation.
Key Points
- To find the X intercept of a function, set the function equal to zero and solve for X.
- For linear functions f(x) = mx + b, the X intercept is X = -b/m.
- For quadratic equations f(x) = ax^2 + bx + c, the X intercept can be found using factoring, completing the square, or the quadratic formula: X = (-b ± √(b^2 - 4ac)) / 2a.
- Understanding the nature of the function (linear, quadratic, polynomial, etc.) is crucial for selecting the appropriate method to find the X intercept.
- X intercepts are significant in graphing functions, as they indicate where the function's graph crosses the X-axis.
Linear Functions and X Intercepts

Linear functions are the simplest case when it comes to finding X intercepts. The general form of a linear function is f(x) = mx + b, where m represents the slope of the line and b represents the Y-intercept. The X intercept occurs where the line crosses the X-axis, meaning f(x) = 0.
By substituting f(x) = 0 into the equation mx + b = 0, we can solve for X to find the X intercept. This yields X = -b/m. For example, if we have the function f(x) = 2x + 4, setting f(x) = 0 gives us 2x + 4 = 0. Solving for X, we get X = -4/2 = -2. Thus, the X intercept of the function f(x) = 2x + 4 is -2.
Quadratic Equations and X Intercepts
Quadratic equations, with the general form f(x) = ax^2 + bx + c, require more sophisticated methods to find their X intercepts. There are three primary methods: factoring, completing the square, and using the quadratic formula.
Factoring involves expressing the quadratic equation as a product of two binomial factors, (x - r)(x - s), where r and s are the roots or X intercepts of the equation. If the equation can be easily factored, this method provides a straightforward way to find the X intercepts.
Completing the square is another method used to find the X intercepts of a quadratic equation. It involves manipulating the equation into a perfect square trinomial form, which can then be easily solved for X.
The quadratic formula, X = (-b ± √(b^2 - 4ac)) / 2a, provides a universal method for finding the X intercepts of any quadratic equation. This formula is derived from completing the square and is applicable to all quadratic equations, regardless of whether they can be factored or not.
| Method | Description |
|---|---|
| Factoring | Expressing the quadratic as a product of two binomials to find roots. |
| Completing the Square | Manipulating the quadratic into a perfect square form to solve for X. |
| Quadratic Formula | Using the formula X = (-b ± √(b^2 - 4ac)) / 2a to find the roots. |

Polynomial Functions and X Intercepts
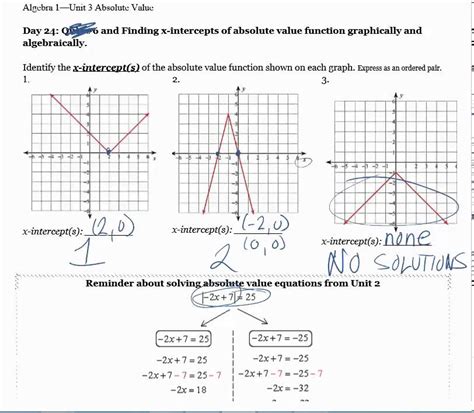
Polynomial functions of degree higher than two introduce additional complexity when finding X intercepts. While the methods for quadratic equations are well-defined, polynomials of degree three or higher may require numerical methods or specialized algebraic techniques to find their roots.
For cubic equations (polynomials of degree three), there are methods like Cardano's Formula, but these become increasingly complex and are less commonly used in basic algebra. For polynomials of even higher degrees, finding X intercepts often involves numerical methods, such as the Newton-Raphson method, or the use of computational tools and graphing calculators.
Understanding the nature of the polynomial and its degree is crucial for determining the best approach to find its X intercepts. Additionally, recognizing that a polynomial of degree n will have up to n real roots (X intercepts) is essential for anticipating the number of solutions.
Numerical Methods for Finding X Intercepts
Numerical methods are often employed for finding the X intercepts of higher-degree polynomials or when an exact algebraic solution is not feasible. These methods include iterative techniques that refine an initial guess until it converges to a root of the equation.
The Newton-Raphson method is a powerful example of a numerical method used for finding roots. It starts with an initial guess, x_0, and iteratively improves this guess using the formula x_{n+1} = x_n - f(x_n) / f'(x_n), where f'(x) is the derivative of the function f(x). This process continues until the difference between successive guesses is less than a predetermined tolerance, indicating convergence to a root.
Other numerical methods, such as the bisection method and the secant method, also exist and are used depending on the specific characteristics of the function and the desired precision of the roots.
What is the significance of finding X intercepts in functions?
+X intercepts are crucial in understanding where a function's graph crosses the X-axis, which can be vital in various mathematical and real-world applications, including graphing, solving equations, and modeling phenomena.
How do I determine the best method for finding X intercepts of a quadratic equation?
+The choice of method depends on the nature of the quadratic equation. If the equation can be easily factored, factoring is the most straightforward method. Otherwise, completing the square or using the quadratic formula may be more appropriate.
Can numerical methods always find the exact X intercepts of a function?
+Numerical methods can find approximate values of X intercepts to a high degree of accuracy but may not always yield the exact values, especially for functions with complex or multiple roots.
In conclusion, finding the X intercepts of functions is a fundamental aspect of algebra and graphing, with applications across various disciplines. The approach to finding X intercepts varies depending on the type of function, ranging from simple linear equations to more complex polynomial functions. Understanding the appropriate methods for different types of functions and being able to apply them effectively is essential for solving equations and analyzing functions in mathematics and science.