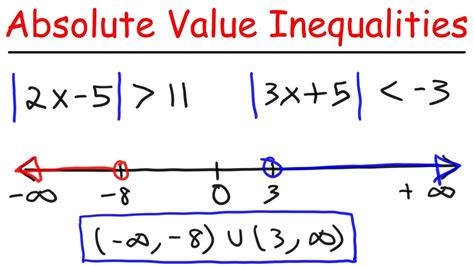
Solving absolute value inequalities is a fundamental concept in algebra, and it can be a challenging topic for many students. However, with a clear understanding of the underlying principles and a step-by-step approach, anyone can master this skill. In this article, we will delve into the world of absolute value inequalities, exploring the different types, solution methods, and providing plenty of examples to illustrate the concepts.
Key Points
- Absolute value inequalities can be solved using the properties of absolute value and the rules of inequalities.
- There are two main types of absolute value inequalities: those with a single absolute value expression and those with multiple absolute value expressions.
- The solution to an absolute value inequality can be expressed as a single interval, a union of intervals, or an empty set.
- Graphing absolute value inequalities on a number line can help visualize the solution set and check for errors.
- Real-world applications of absolute value inequalities include optimization problems, distance and rate problems, and modeling uncertain or noisy data.
Understanding Absolute Value Inequalities
Absolute value inequalities are statements that involve the absolute value of an expression and a comparison operator, such as less than, greater than, less than or equal to, or greater than or equal to. The absolute value of a number is its distance from zero on the number line, regardless of direction. For example, the absolute value of -3 is 3, and the absolute value of 3 is also 3.
The key to solving absolute value inequalities is to use the properties of absolute value and the rules of inequalities. One important property is that the absolute value of a product is equal to the product of the absolute values. This means that |ab| = |a||b|. Another important property is that the absolute value of a sum or difference is less than or equal to the sum of the absolute values. This means that |a + b| ≤ |a| + |b| and |a - b| ≤ |a| + |b|.
Solving Absolute Value Inequalities with a Single Absolute Value Expression
When solving an absolute value inequality with a single absolute value expression, we can use the following steps:
Step 1: Isolate the absolute value expression on one side of the inequality.
Step 2: Set up two separate inequalities, one without the absolute value and one with the absolute value.
Step 3: Solve each inequality separately and combine the solutions.
For example, consider the inequality |x - 2| < 3. To solve this inequality, we would first isolate the absolute value expression on one side: |x - 2| < 3. Then, we would set up two separate inequalities: x - 2 < 3 and x - 2 > -3. Solving each inequality separately, we get x < 5 and x > -1. Combining the solutions, we get -1 < x < 5.
| Type of Inequality | Example | Solution |
|---|---|---|
| Absolute value inequality with a single absolute value expression | |x - 2| < 3 | -1 < x < 5 |
| Absolute value inequality with multiple absolute value expressions | |x - 2| + |x + 1| > 5 | x < -3 or x > 2 |

Solving Absolute Value Inequalities with Multiple Absolute Value Expressions

When solving an absolute value inequality with multiple absolute value expressions, we need to use a different approach. One way to solve these types of inequalities is to use the properties of absolute value and the rules of inequalities to simplify the inequality and then solve it.
For example, consider the inequality |x - 2| + |x + 1| > 5. To solve this inequality, we would first simplify the left-hand side by using the properties of absolute value: |x - 2| + |x + 1| = |x - 2| + |-(x + 1)| = |x - 2| + |-1||x + 1| = |x - 2| + |x + 1|. Then, we would solve the inequality |x - 2| + |x + 1| > 5.
To solve this inequality, we can use the following steps:
Step 1: Find the critical points of the inequality by setting each absolute value expression equal to zero and solving for x.
Step 2: Use the critical points to divide the number line into intervals and test each interval to see where the inequality is satisfied.
Using these steps, we can solve the inequality |x - 2| + |x + 1| > 5 and find the solution set.
Graphing Absolute Value Inequalities on a Number Line
Graphing absolute value inequalities on a number line can help visualize the solution set and check for errors. To graph an absolute value inequality, we can use the following steps:
Step 1: Find the critical points of the inequality by setting each absolute value expression equal to zero and solving for x.
Step 2: Plot the critical points on a number line.
Step 3: Test each interval to see where the inequality is satisfied.
Step 4: Shade the intervals where the inequality is satisfied.
By graphing absolute value inequalities on a number line, we can quickly and easily visualize the solution set and check for errors.
What is the difference between an absolute value equation and an absolute value inequality?
+An absolute value equation is a statement that involves the absolute value of an expression and an equal sign, whereas an absolute value inequality is a statement that involves the absolute value of an expression and a comparison operator, such as less than, greater than, less than or equal to, or greater than or equal to.
How do I solve an absolute value inequality with multiple absolute value expressions?
+To solve an absolute value inequality with multiple absolute value expressions, we can use the properties of absolute value and the rules of inequalities to simplify the inequality and then solve it. We can also use graphing to visualize the solution set and check for errors.
What are some real-world applications of absolute value inequalities?
+Absolute value inequalities have many real-world applications, including optimization problems, distance and rate problems, and modeling uncertain or noisy data. They are used in fields such as physics, engineering, economics, and computer science.