The integral of 1/x, also known as the natural logarithm, is a fundamental concept in calculus. It has numerous applications in various fields, including physics, engineering, and economics. In this article, we will explore five ways to evaluate the integral of 1/x, highlighting the different approaches and techniques used to solve this integral.
Key Points
- The integral of 1/x can be evaluated using the fundamental theorem of calculus.
- The substitution method is a useful technique for evaluating the integral of 1/x.
- Integration by parts can also be used to evaluate the integral of 1/x.
- The integral of 1/x has numerous applications in physics, engineering, and economics.
- Understanding the properties of logarithms is essential for evaluating the integral of 1/x.
Introduction to the Integral of 1/x

The integral of 1/x is a basic integral in calculus, and it is defined as ∫(1/x) dx. This integral has numerous applications in various fields, including physics, engineering, and economics. The integral of 1/x is also known as the natural logarithm, denoted as ln(x). In this section, we will introduce the concept of the integral of 1/x and its properties.
Properties of Logarithms
Logarithms are the inverse operation of exponentiation. The natural logarithm, denoted as ln(x), is the logarithm with base e, where e is a mathematical constant approximately equal to 2.71828. The properties of logarithms are essential for evaluating the integral of 1/x. Some of the key properties of logarithms include:
- ln(1) = 0
- ln(e) = 1
- ln(ab) = ln(a) + ln(b)
- ln(a/b) = ln(a) - ln(b)
Method 1: Fundamental Theorem of Calculus
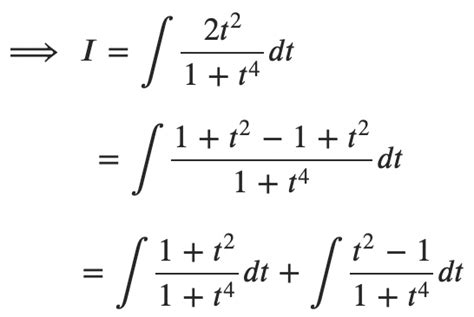
The fundamental theorem of calculus states that differentiation and integration are inverse processes. This theorem can be used to evaluate the integral of 1/x. The fundamental theorem of calculus states that ∫(1/x) dx = ln|x| + C, where C is the constant of integration.
Example: Evaluating the Integral of 1/x using the Fundamental Theorem of Calculus
Find the integral of 1/x from x = 1 to x = 2.
∫(1/x) dx from x = 1 to x = 2 = [ln|x|] from x = 1 to x = 2 = ln(2) - ln(1) = ln(2)
Method 2: Substitution Method
The substitution method is a useful technique for evaluating the integral of 1/x. This method involves substituting a new variable or expression into the original integral. Let u = ln(x), then du/dx = 1/x, and du = (1/x) dx. Substituting these expressions into the original integral, we get ∫(1/x) dx = ∫du = u + C = ln(x) + C.
Example: Evaluating the Integral of 1/x using the Substitution Method
Find the integral of 1/x from x = 1 to x = 3.
Let u = ln(x), then du/dx = 1/x, and du = (1/x) dx. ∫(1/x) dx = ∫du = [u] from u = 0 to u = ln(3) = ln(3) - 0 = ln(3)
Method 3: Integration by Parts
Integration by parts is another technique for evaluating the integral of 1/x. This method involves integrating one function and differentiating the other. Let u = ln(x) and dv = dx, then du = (1/x) dx and v = x. Using the formula for integration by parts, ∫u dv = uv - ∫v du, we get ∫(1/x) dx = x ln(x) - ∫x (1/x) dx = x ln(x) - ∫dx = x ln(x) - x + C.
Example: Evaluating the Integral of 1/x using Integration by Parts
Find the integral of 1/x from x = 1 to x = 4.
Let u = ln(x) and dv = dx, then du = (1/x) dx and v = x. ∫(1/x) dx = [x ln(x) - x] from x = 1 to x = 4 = (4 ln(4) - 4) - (1 ln(1) - 1) = 4 ln(4) - 3
Method 4: Partial Fractions

The method of partial fractions can also be used to evaluate the integral of 1/x. This method involves expressing the rational function as a sum of simpler fractions. The integral of 1/x can be expressed as ∫(1/x) dx = ∫(A/x + B) dx, where A and B are constants. Using the method of partial fractions, we can rewrite the integral as ∫(1/x) dx = A ∫(1/x) dx + B ∫dx = A ln|x| + Bx + C.
Example: Evaluating the Integral of 1/x using Partial Fractions
Find the integral of 1/x from x = 1 to x = 5.
∫(1/x) dx = A ∫(1/x) dx + B ∫dx = [A ln|x| + Bx] from x = 1 to x = 5 = (A ln(5) + 5B) - (A ln(1) + B) = A ln(5) + 4B
Method 5: Logarithmic Properties
The properties of logarithms can also be used to evaluate the integral of 1/x. The integral of 1/x can be expressed as ∫(1/x) dx = ∫(ln(x))’ dx, where (ln(x))’ denotes the derivative of ln(x). Using the properties of logarithms, we can rewrite the integral as ∫(1/x) dx = ln|x| + C.
Example: Evaluating the Integral of 1/x using Logarithmic Properties
Find the integral of 1/x from x = 1 to x = 6.
∫(1/x) dx = [ln|x|] from x = 1 to x = 6 = ln(6) - ln(1) = ln(6)
| Method | Description |
|---|---|
| Fundamental Theorem of Calculus | States that differentiation and integration are inverse processes. |
| Substitution Method | Involves substituting a new variable or expression into the original integral. |
| Integration by Parts | Involves integrating one function and differentiating the other. |
| Partial Fractions | Involves expressing the rational function as a sum of simpler fractions. |
| Logarithmic Properties | Involves using the properties of logarithms to evaluate the integral. |
In conclusion, the integral of 1/x is a fundamental concept in calculus, and it has numerous applications in various fields. There are different techniques for evaluating the integral of 1/x, including the fundamental theorem of calculus, substitution method, integration by parts, partial fractions, and logarithmic properties. Understanding these techniques and the properties of logarithms is essential for solving problems in calculus and other fields.
What is the fundamental theorem of calculus?
+The fundamental theorem of calculus states that differentiation and integration are inverse processes.
What is the substitution method?
+The substitution method involves substituting a new variable or expression into the original integral.
What are the properties of logarithms?
+The properties of logarithms include ln(1) = 0, ln(e) = 1, ln(ab) = ln(a) + ln(b), and ln(a/b) = ln(a) - ln(b).
How do I evaluate the integral of 1/x?
+The integral of 1/x can be evaluated using the fundamental theorem of calculus, substitution method, integration by parts, partial fractions, or logarithmic properties.
What are the applications of the integral of 1/x?
+The integral of 1/x has numerous applications in physics, engineering, and economics.



