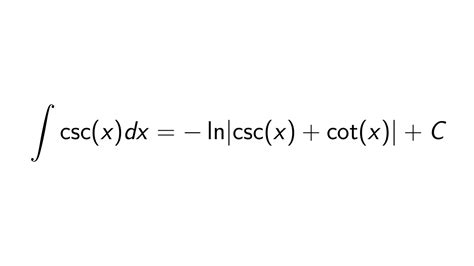The integral of csc, or cosecant, is a fundamental concept in calculus, particularly in the realm of trigonometric integrals. Cosecant, denoted as csc(x), is the reciprocal of sine, or 1/sin(x). Integrating csc(x) involves understanding its relationship with other trigonometric functions and applying appropriate integration techniques. In this explanation, we will delve into the process of integrating csc(x) and explore its applications.
Understanding Csc(x) and Its Integral

To integrate csc(x), it’s crucial to recall the definition of csc(x) as 1/sin(x). The integral of csc(x) is given by ∫csc(x) dx. To solve this, we can utilize the relationship between csc(x) and the natural logarithm function, alongside the properties of trigonometric identities. Specifically, we can leverage the identity that involves the derivative of the natural logarithm of the tangent function, which is related to csc(x) through trigonometric identities.
Derivation of the Integral of Csc(x)
The derivation begins with recognizing that the derivative of ln|tan(x/2)| can be manipulated to express csc(x). Using the half-angle formula for tangent, tan(x/2) = sin(x) / (1 + cos(x)), we can derive the expression for csc(x) in terms of ln|tan(x/2)|. By differentiating ln|tan(x/2)| with respect to x, we apply the chain rule and simplify using trigonometric identities to arrive at an expression that relates to csc(x). This process involves understanding that d(ln|tan(x/2)|)/dx = (1/sin(x)) * (1 + cos(x))/(1 + cos(x)) = csc(x), thus providing a pathway to integrate csc(x) by relating it to the natural logarithm of the tangent of half the angle.
| Trigonometric Function | Integral Form |
|---|---|
| csc(x) | -ln|csc(x) + cot(x)| + C |
| sin(x) | -cos(x) + C |
| cos(x) | sin(x) + C |
Applications and Interpretations
The integral of csc(x) has various applications in physics, engineering, and other fields where trigonometric functions model periodic phenomena. For instance, in the study of pendulum motion, the equation of motion can involve trigonometric functions, and understanding their integrals is crucial for analyzing the pendulum’s behavior over time. Additionally, in electrical engineering, the analysis of circuits involving AC (alternating current) sources may require the integration of trigonometric functions, including csc(x), to determine voltage, current, and power relationships.
Key Points
- The integral of csc(x) is -ln|csc(x) + cot(x)| + C, derived from the relationship between csc(x) and the natural logarithm of the tangent of half the angle.
- Csc(x) is the reciprocal of sin(x), and its integral is essential in various applications, including physics and engineering.
- Understanding trigonometric identities and their derivatives is crucial for integrating csc(x) and other trigonometric functions.
- The integral of csc(x) has applications in modeling periodic phenomena and analyzing systems that involve AC sources.
- Recognizing the absolute value in the integral's result ensures the formula's applicability across the domain of csc(x) and cot(x).
In conclusion, the integral of csc(x) is a fundamental concept that relies on understanding the intricate relationships between trigonometric functions and their derivatives. By recognizing these relationships and applying appropriate integration techniques, we can derive the integral of csc(x) and explore its applications in various fields. The integration of csc(x) not only demonstrates the beauty of calculus in simplifying complex problems but also highlights the importance of trigonometric functions in modeling real-world phenomena.
What is the integral of csc(x), and how is it derived?
+The integral of csc(x) is -ln|csc(x) + cot(x)| + C. It is derived by utilizing the relationship between csc(x) and the natural logarithm of the tangent of half the angle, along with trigonometric identities and the chain rule in differentiation.
What are some applications of the integral of csc(x)?
+The integral of csc(x) has applications in physics, particularly in the study of pendulum motion, and in electrical engineering, especially in the analysis of AC circuits.
Why is the absolute value important in the integral of csc(x)?
+The absolute value in -ln|csc(x) + cot(x)| + C ensures that the result is defined for all x where csc(x) and cot(x) are defined, making the formula applicable across their domain.