The multiplicative inverse property is a fundamental concept in mathematics, particularly in algebra and number theory. It states that for every non-zero number, there exists a multiplicative inverse, which when multiplied by the original number, results in the product being equal to 1. In other words, if we have a number $a$, then its multiplicative inverse is denoted as $\frac{1}{a}$ or $a^{-1}$, and the product of $a$ and its inverse is equal to 1, i.e., $a \cdot \frac{1}{a} = 1$. This property is essential in various mathematical operations, including solving equations, simplifying expressions, and performing arithmetic calculations.
Key Points
- The multiplicative inverse property applies to all non-zero numbers, including integers, fractions, decimals, and complex numbers.
- The multiplicative inverse of a number $a$ is denoted as $\frac{1}{a}$ or $a^{-1}$.
- The product of a number and its multiplicative inverse is equal to 1, i.e., $a \cdot \frac{1}{a} = 1$.
- The multiplicative inverse property is used to solve equations, simplify expressions, and perform arithmetic calculations.
- The property is essential in various mathematical fields, including algebra, calculus, and number theory.
Multiplicative Inverse Property Definition and Examples

The multiplicative inverse property can be defined as follows: for every non-zero number a, there exists a number b such that a \cdot b = 1. The number b is called the multiplicative inverse of a, denoted as \frac{1}{a} or a^{-1}. For example, the multiplicative inverse of 2 is \frac{1}{2}, since 2 \cdot \frac{1}{2} = 1. Similarly, the multiplicative inverse of \frac{3}{4} is \frac{4}{3}, since \frac{3}{4} \cdot \frac{4}{3} = 1.
Multiplicative Inverse Property in Different Number Systems
The multiplicative inverse property applies to various number systems, including integers, fractions, decimals, and complex numbers. In the integer number system, the multiplicative inverse of a number a is denoted as \frac{1}{a}, and it is defined as the integer that, when multiplied by a, results in the product being equal to 1. For example, the multiplicative inverse of 3 is \frac{1}{3}, since 3 \cdot \frac{1}{3} = 1. In the fraction number system, the multiplicative inverse of a fraction \frac{a}{b} is denoted as \frac{b}{a}, and it is defined as the fraction that, when multiplied by \frac{a}{b}, results in the product being equal to 1.
| Number System | Multiplicative Inverse Example |
|---|---|
| Integers | 2 and $\frac{1}{2}$, since $2 \cdot \frac{1}{2} = 1$ |
| Fractions | $\frac{3}{4}$ and $\frac{4}{3}$, since $\frac{3}{4} \cdot \frac{4}{3} = 1$ |
| Decimals | 0.5 and 2, since $0.5 \cdot 2 = 1$ |
| Complex Numbers | $i$ and $-i$, since $i \cdot -i = 1$ |

Applications of the Multiplicative Inverse Property
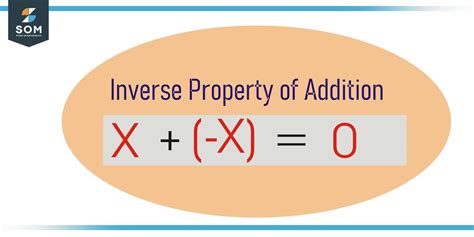
The multiplicative inverse property has numerous applications in mathematics and other fields. One of the most significant applications is in solving equations, particularly linear equations. For example, to solve the equation 2x = 3, we can multiply both sides of the equation by the multiplicative inverse of 2, which is \frac{1}{2}. This results in x = \frac{3}{2}, which is the solution to the equation. Another application of the multiplicative inverse property is in simplifying expressions, such as \frac{2}{3} \cdot \frac{3}{2}, which simplifies to 1.
Multiplicative Inverse Property in Calculus and Number Theory
The multiplicative inverse property also has significant applications in calculus and number theory. In calculus, the property is used to find the derivatives and integrals of functions, particularly those involving trigonometric and exponential functions. For example, the derivative of the function f(x) = \frac{1}{x} is f'(x) = -\frac{1}{x^2}, which can be found using the multiplicative inverse property. In number theory, the property is used to study the properties of integers and modular arithmetic, particularly in the context of cryptography and coding theory.
What is the multiplicative inverse property?
+The multiplicative inverse property states that for every non-zero number, there exists a multiplicative inverse, which when multiplied by the original number, results in the product being equal to 1.
What is the multiplicative inverse of a number?
+The multiplicative inverse of a number a is denoted as \frac{1}{a} or a^{-1}, and it is defined as the number that, when multiplied by a, results in the product being equal to 1.
What are the applications of the multiplicative inverse property?
+The multiplicative inverse property has numerous applications in mathematics and other fields, including solving equations, simplifying expressions, and performing arithmetic calculations.