The concept of negative times positive is a fundamental aspect of mathematics, particularly in the realm of algebra and arithmetic. It is essential to understand the rules and principles governing the multiplication of negative and positive numbers to perform calculations accurately. In this explanation, we will delve into the world of negative times positive, exploring the underlying principles, rules, and practical applications.
Key Points
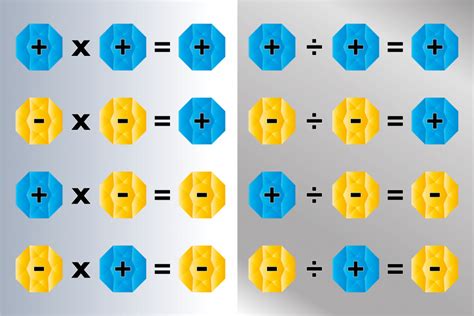
- The product of a negative number and a positive number is always negative.
- The rule for multiplying negative and positive numbers is based on the concept of direction and magnitude.
- Understanding the concept of negative times positive is crucial for solving algebraic equations and inequalities.
- Real-world applications of negative times positive include finance, physics, and engineering.
- Mastering the concept of negative times positive is essential for developing problem-solving skills in mathematics.
Understanding the Concept of Negative Times Positive

To comprehend the concept of negative times positive, it is vital to grasp the basic principles of multiplication. When we multiply two numbers, we are essentially adding a number a certain number of times. For instance, 3 × 4 means adding 3 together 4 times, resulting in 12. However, when we introduce negative numbers into the equation, the rules change slightly.
A negative number represents a direction or magnitude opposite to that of a positive number. When we multiply a negative number by a positive number, we are essentially changing the direction of the result. To illustrate this, consider the example of -3 × 4. In this case, we are adding -3 together 4 times, resulting in -12. This demonstrates that the product of a negative number and a positive number is always negative.
The Rule for Multiplying Negative and Positive Numbers
The rule for multiplying negative and positive numbers is straightforward: the product of a negative number and a positive number is always negative. This can be represented mathematically as:
-a × b = -ab
where a and b are positive numbers. This rule applies universally, regardless of the magnitude or direction of the numbers involved.
| Example | Calculation | Result |
|---|---|---|
| -2 × 5 | -2 + (-2) + (-2) + (-2) + (-2) | -10 |
| -4 × 3 | -4 + (-4) + (-4) | -12 |
| -1 × 9 | -1 + (-1) + (-1) + (-1) + (-1) + (-1) + (-1) + (-1) + (-1) | -9 |

Practical Applications of Negative Times Positive

The concept of negative times positive has numerous practical applications in various fields, including finance, physics, and engineering. In finance, negative times positive is used to calculate losses or debts. For instance, if an investor loses 500 on a trade, the calculation would be -500 × 1 = -500, indicating a loss of 500.
In physics, negative times positive is used to calculate forces and velocities. For example, if an object is moving in the opposite direction to the force applied, the calculation would involve negative times positive. This demonstrates the importance of understanding the concept of negative times positive in real-world applications.
Real-World Examples of Negative Times Positive
Real-world examples of negative times positive include:
- Finance: calculating losses or debts
- Physics: calculating forces and velocities
- Engineering: designing and optimizing systems
- Economics: analyzing market trends and predicting outcomes
These examples illustrate the significance of understanding the concept of negative times positive in various fields. By mastering this concept, individuals can develop problem-solving skills and apply mathematical principles to real-world problems.
What is the rule for multiplying negative and positive numbers?
+The rule for multiplying negative and positive numbers is that the product is always negative. This can be represented mathematically as -a × b = -ab, where a and b are positive numbers.
What are some practical applications of negative times positive?
+Practical applications of negative times positive include finance, physics, and engineering. In finance, it is used to calculate losses or debts. In physics, it is used to calculate forces and velocities. In engineering, it is used to design and optimize systems.
Why is it essential to understand the concept of negative times positive?
+Understanding the concept of negative times positive is crucial for developing problem-solving skills in mathematics. It has numerous practical applications in various fields and is essential for making accurate calculations and predictions.
In conclusion, the concept of negative times positive is a fundamental aspect of mathematics, and understanding its principles and rules is essential for making accurate calculations and predictions. By mastering this concept, individuals can develop problem-solving skills and apply mathematical principles to real-world problems. The practical applications of negative times positive are numerous, and its significance extends beyond mathematics to various fields, including finance, physics, and engineering.