When considering mathematical transformations, particularly those involving reflections, it's essential to grasp the concept of reflecting functions over the y-axis. This operation involves changing the sign of the x-variable in the function, which effectively flips the graph of the function horizontally. The transformation is represented by replacing x with -x in the function's equation. For instance, if we have a function f(x), its reflection over the y-axis would be f(-x). This concept is fundamental in algebra and geometry, as it helps in understanding symmetry and manipulating functions to represent real-world phenomena or to simplify complex equations.
Understanding Reflection Over the Y-Axis
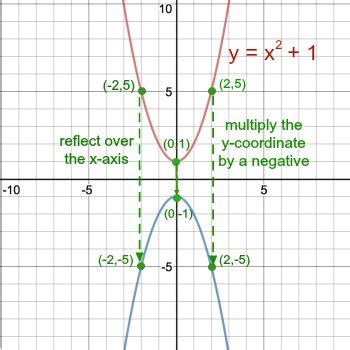
To delve deeper into reflections over the y-axis, let’s consider the impact of this transformation on various types of functions. For linear functions, such as y = mx + b, where m is the slope and b is the y-intercept, reflecting over the y-axis results in y = -mx + b. This shows that the slope’s sign changes, indicating a flip in the line’s direction while the y-intercept remains unchanged. For quadratic functions, like y = ax^2 + bx + c, the reflection leads to y = a(-x)^2 + b(-x) + c, simplifying to y = ax^2 - bx + c, where the coefficient of the x term changes sign but the quadratic term’s coefficient remains the same.
Applications of Reflection in Mathematics
The concept of reflection over the y-axis has numerous applications in mathematics and other fields. In graphing, it helps in identifying and creating symmetric figures, which is crucial for understanding geometric properties and transformations. In calculus, reflections can be used to analyze the behavior of functions and their derivatives, aiding in the study of maxima, minima, and points of inflection. Moreover, reflections are integral in the study of trigonometry, where the periodic nature of trigonometric functions can be understood through reflections and translations.
| Function Type | Original Function | Reflected Function |
|---|---|---|
| Linear | y = mx + b | y = -mx + b |
| Quadratic | y = ax^2 + bx + c | y = ax^2 - bx + c |
| Cubic | y = ax^3 + bx^2 + cx + d | y = -ax^3 + bx^2 - cx + d |
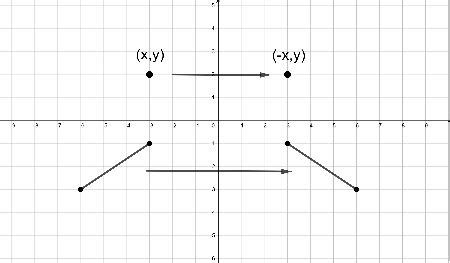
Key Points
- The reflection of a function f(x) over the y-axis is represented by f(-x), involving a change in the sign of the x-variable.
- For linear functions, reflection over the y-axis changes the slope's sign but keeps the y-intercept constant.
- Quadratic functions, when reflected, change the sign of the coefficient of the linear term but keep the quadratic term's coefficient unchanged.
- Reflections have broad applications in mathematics, including graphing, calculus, and trigonometry, aiding in the analysis of functions and their properties.
- Understanding reflections and symmetry is crucial for grasping geometric transformations and for modeling various phenomena in physics, engineering, and other fields.
Advanced Applications and Considerations
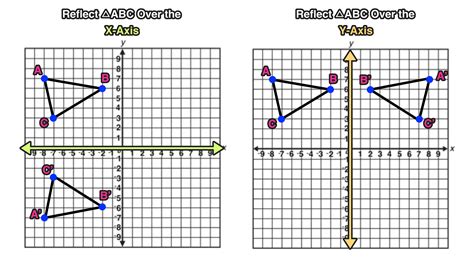
Beyond the basic concept of reflection, there are more complex transformations and considerations, especially when dealing with higher-degree polynomials, rational functions, and trigonometric functions. The reflection of these functions requires a deeper understanding of algebraic manipulation and the properties of functions. Furthermore, in three-dimensional space, reflections can occur over planes, adding another layer of complexity to the transformations. The study of these advanced transformations is essential for advancements in fields like computer graphics, where realistic rendering of reflections and other effects is critical.
Reflections in Real-World Scenarios
In real-world applications, reflections are not limited to mathematical functions. They appear in physics, particularly in optics, where the reflection of light off surfaces is a fundamental principle. The behavior of light as it reflects off mirrors or other surfaces can be described using the principles of geometric optics. Additionally, in materials science, the reflection of waves, whether sound or light, is crucial for understanding the properties of materials and designing new technologies, such as reflective coatings or acoustic barriers.
What is the effect of reflecting a linear function over the y-axis?
+The reflection of a linear function y = mx + b over the y-axis changes the slope's sign, resulting in y = -mx + b, but keeps the y-intercept constant.
How does the reflection over the y-axis affect a quadratic function?
+For a quadratic function y = ax^2 + bx + c, reflection over the y-axis results in y = ax^2 - bx + c, where the coefficient of the x term changes sign, but the quadratic term's coefficient remains unchanged.
What are some real-world applications of reflections in mathematics and physics?
+Reflections have applications in graphing and understanding symmetric properties, calculus for analyzing function behavior, trigonometry for understanding periodic functions, physics for describing the behavior of light and sound, and materials science for designing reflective technologies.
In conclusion, reflections over the y-axis are a fundamental concept in mathematics, with applications spanning across various disciplines. Understanding how different functions behave under reflection is crucial for deeper insights into their properties and for modeling real-world phenomena. By recognizing the significance of reflections in mathematics and beyond, we can better appreciate the interconnectedness of concepts and the importance of mathematical principles in describing our world.