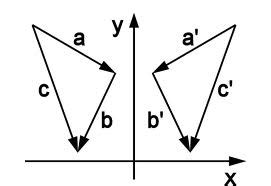
Reflection, in the context of mathematics, refers to a transformation that flips a figure over a line of reflection, which can be a horizontal line, a vertical line, or even a diagonal line. This concept is fundamental in geometry and is used to describe the symmetry of objects. When a figure is reflected, each point of the figure is mapped to a corresponding point on the opposite side of the line of reflection, with the line of reflection acting as the mirror. The original figure and its reflection are congruent, meaning they have the same size and shape, but they are not necessarily in the same position.
The mathematical definition of reflection involves understanding the concept of line symmetry. Line symmetry exists when a figure can be divided into two congruent parts by a line, with one part being a reflection of the other. This line is the line of reflection or axis of symmetry. Reflections can be performed in various directions - horizontally, vertically, or along any other line. In each case, the line of reflection remains unchanged, and the figure is flipped over this line to create its mirror image.
Key Points
- Reflection in mathematics is a transformation that flips a figure over a line of reflection.
- The line of reflection can be horizontal, vertical, or diagonal.
- The original figure and its reflection are congruent, having the same size and shape but not necessarily the same position.
- Reflection is used to describe the symmetry of objects, with line symmetry being a key concept.
- Reflections can be performed in various directions, with the line of reflection remaining unchanged.
Understanding Reflection in Geometry
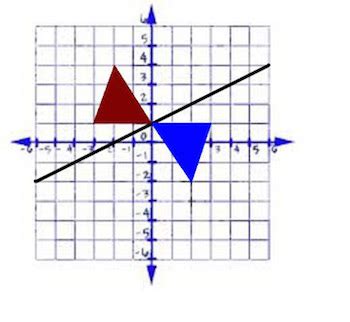
Geometry, the branch of mathematics that deals with the properties, measurement, and relationships of points, lines, angles, and solids, heavily utilizes the concept of reflection. In geometry, reflections are used to create symmetries, which are essential for understanding the properties of geometric figures. For instance, a rectangle has two lines of symmetry - one vertical and one horizontal. When a rectangle is reflected over its vertical line of symmetry, the left and right halves of the rectangle are mirror images of each other. Similarly, reflecting a rectangle over its horizontal line of symmetry creates mirror images of the top and bottom halves.
Types of Reflections
There are several types of reflections, each defined by the orientation of the line of reflection. Horizontal reflections flip a figure over a horizontal line, while vertical reflections flip a figure over a vertical line. Diagonal reflections, on the other hand, flip a figure over a diagonal line. Understanding these types of reflections is crucial for analyzing the symmetry of geometric figures and for performing geometric transformations.
| Type of Reflection | Description |
|---|---|
| Horizontal Reflection | Flips a figure over a horizontal line. |
| Vertical Reflection | Flips a figure over a vertical line. |
| Diagonal Reflection | Flips a figure over a diagonal line. |
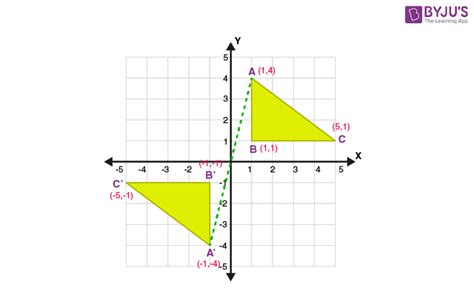
Applications of Reflection in Mathematics and Beyond
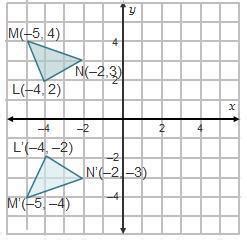
Reflections have numerous applications in mathematics and other fields. In mathematics, reflections are used in geometry to study the properties of figures and their symmetries. They are also essential in trigonometry and algebra, where they help in solving equations and understanding functions. Beyond mathematics, reflections are used in art to create symmetrical compositions, in architecture to design buildings with balanced facades, and in engineering to design symmetric structures that are stronger and more stable.
Reflection in Real-World Scenarios
In real-world scenarios, reflections are observed in the symmetry of nature, such as in the structure of flowers, the arrangement of leaves on stems, and the symmetry of animal bodies. Reflections are also used in technology, for example, in the design of symmetric algorithms for data encryption and in the creation of mirror-like finishes on electronic devices. The concept of reflection, therefore, extends far beyond the realm of mathematics, influencing various aspects of human creativity and innovation.
What is the mathematical definition of reflection?
+Reflection, in mathematics, refers to a transformation that flips a figure over a line of reflection, creating a mirror image of the original figure. The original and reflected figures are congruent but not necessarily in the same position.
What are the types of reflections in geometry?
+The main types of reflections in geometry are horizontal, vertical, and diagonal reflections, each defined by the orientation of the line of reflection over which the figure is flipped.
What are the practical applications of reflections?
+Reflections have practical applications in various fields, including art, architecture, engineering, and technology. They are used to create symmetrical compositions, design balanced structures, and develop symmetric algorithms for data encryption, among other uses.