Algebra 2 is a fundamental course in mathematics that builds upon the principles of algebra, introducing students to more complex concepts such as quadratic equations, functions, and graphing. Mastering Algebra 2 is crucial for students who wish to pursue higher-level math courses, such as calculus, and for those interested in careers in science, technology, engineering, and mathematics (STEM). To excel in Algebra 2, it's essential to have a solid grasp of the basics and to develop effective study habits. Here are five tips to help you succeed in Algebra 2.
Key Points
- Understand the fundamentals of algebra, including solving linear equations and graphing lines.
- Practice consistently to develop problem-solving skills and to become familiar with different types of equations and functions.
- Use visual aids like graphs and charts to help understand complex concepts.
- Break down complex problems into simpler steps to make them more manageable.
- Seek help when needed, whether from a teacher, tutor, or classmate, to clarify any misunderstandings.
Understanding Quadratic Equations

Quadratic equations are a critical component of Algebra 2, and understanding how to solve them is vital. A quadratic equation is in the form of (ax^2 + bx + c = 0), where (a), (b), and (c) are constants, and (x) is the variable. There are several methods to solve quadratic equations, including factoring, the quadratic formula, and graphing. The quadratic formula, (x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}), is particularly useful when the equation cannot be easily factored. Practicing solving quadratic equations will help you become proficient in recognizing the best method to use for different types of problems.
Graphing Functions
Graphing functions is another essential skill in Algebra 2. It involves plotting points on a coordinate plane to visualize the behavior of a function. Understanding how to graph different types of functions, such as linear, quadratic, and polynomial functions, can help you identify key characteristics, such as the vertex, axis of symmetry, and intercepts. Graphing calculators can be powerful tools for exploring functions and visualizing complex relationships, but it’s also important to learn how to graph functions by hand to understand the underlying mathematics.
| Type of Function | Characteristics |
|---|---|
| Linear Function | Constant rate of change, straight line |
| Quadratic Function | Parabolic shape, one vertex, axis of symmetry |
| Polynomial Function | Varies, can have multiple roots and turning points |
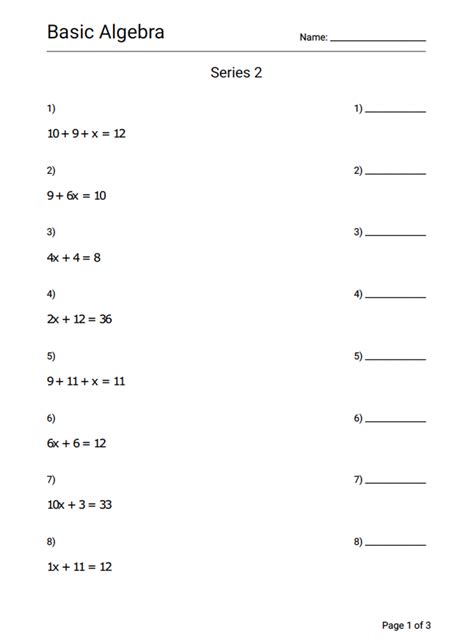
Systems of Equations

Solving systems of equations is another critical skill in Algebra 2. A system of equations involves two or more equations that have the same variables. There are several methods to solve systems of equations, including substitution, elimination, and graphing. The method you choose depends on the complexity of the equations and your personal preference. For example, if one of the equations is already solved for one variable, substitution might be the easiest method. However, if the coefficients of one of the variables are the same in both equations, elimination could be more straightforward.
Functions and Relations
Understanding the difference between functions and relations is also important in Algebra 2. A function is a relation between a set of inputs (called the domain) and a set of possible outputs (called the range), where each input is related to exactly one output. A relation, on the other hand, can have multiple outputs for a single input. Identifying whether a relation represents a function can be done by using the vertical line test on its graph: if a vertical line intersects the graph at more than one point, the relation is not a function.
As you progress through Algebra 2, you'll encounter more advanced topics, such as exponential and logarithmic functions, and you'll learn how to apply mathematical models to real-world problems. Remember, practice is key to mastering these concepts. Consistently working on problems and seeking help when you're unsure will help you build a strong foundation in algebra and prepare you for future math courses.
What is the quadratic formula used for?
+The quadratic formula is used to solve quadratic equations of the form (ax^2 + bx + c = 0). It provides the solutions to the equation, giving the values of (x).
How do I graph a function?
+To graph a function, you can use a graphing calculator or plot points on a coordinate plane. First, identify key points such as the y-intercept, x-intercepts, and any vertices or turning points. Then, use these points to sketch the graph, ensuring it passes through all the identified points and behaves as expected between them.
What is the difference between a function and a relation?
+A function is a special type of relation where each input (or element of the domain) is associated with exactly one output (or element of the range). A relation, however, can have multiple outputs for a single input.



