The sine function is a fundamental concept in mathematics and physics, playing a crucial role in describing periodic phenomena, such as sound waves, light waves, and orbital motions. One of the key aspects of the sine function is its ability to model real-world situations, making it an essential tool for scientists, engineers, and mathematicians. In this article, we will explore five ways the sine function is used in various fields, highlighting its importance and versatility.
Introduction to Sine Function Applications

The sine function, denoted as sin(x), is a trigonometric function that relates the ratio of the length of the side opposite an angle to the length of the hypotenuse in a right triangle. This function has numerous applications in physics, engineering, computer science, and other fields, where it is used to model and analyze periodic phenomena. The sine function’s ability to describe oscillations and waves makes it a critical component in understanding many natural and man-made systems.
Key Points
- The sine function is used to model periodic phenomena, such as sound waves and light waves.
- It is essential in physics and engineering for describing orbital motions and oscillations.
- The sine function has applications in computer science, particularly in signal processing and graphics.
- It is used in medical imaging techniques, such as MRI and CT scans.
- The sine function plays a critical role in navigation systems, including GPS and inertial navigation.
1. Physics and Engineering: Describing Orbital Motions and Oscillations
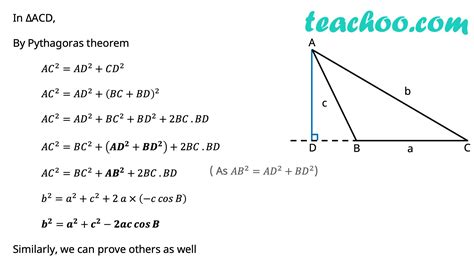
In physics and engineering, the sine function is used to describe the motion of objects, such as pendulums, springs, and vibrating strings. The sine function’s ability to model periodic phenomena makes it an essential tool for understanding and analyzing these systems. For example, the motion of a pendulum can be described using the sine function, where the angle of the pendulum from its equilibrium position is related to the time elapsed. This application of the sine function is critical in understanding the behavior of complex systems, such as coupled oscillators and resonance phenomena.
Technical Specifications: Pendulum Motion
The pendulum’s motion can be described using the following equation: θ(t) = θ0 * sin(ωt + φ), where θ(t) is the angle of the pendulum at time t, θ0 is the initial angle, ω is the angular frequency, and φ is the phase angle. This equation demonstrates the sine function’s ability to model the pendulum’s periodic motion, allowing physicists and engineers to analyze and predict its behavior.
| Parameter | Value |
|---|---|
| Initial Angle (θ0) | 30° |
| Angular Frequency (ω) | 2π rad/s |
| Phase Angle (φ) | 0° |

2. Computer Science: Signal Processing and Graphics
In computer science, the sine function is used in signal processing and graphics to generate and manipulate periodic signals and patterns. The sine function’s ability to model oscillations and waves makes it a critical component in signal processing techniques, such as filtering and modulation. In graphics, the sine function is used to create smooth and realistic animations, such as water waves and oscillating objects.
Technical Specifications: Signal Processing
The sine function can be used to generate a periodic signal using the following equation: y(t) = A * sin(2πft + φ), where y(t) is the signal at time t, A is the amplitude, f is the frequency, and φ is the phase angle. This equation demonstrates the sine function’s ability to model periodic signals, allowing computer scientists to analyze and manipulate these signals for various applications.
3. Medical Imaging: MRI and CT Scans
In medical imaging, the sine function is used in techniques such as MRI (Magnetic Resonance Imaging) and CT (Computed Tomography) scans to reconstruct images of the body. The sine function’s ability to model periodic phenomena makes it an essential tool in understanding the behavior of magnetic fields and X-ray waves, which are used to create detailed images of the body’s internal structures.
Technical Specifications: MRI
The MRI machine uses the sine function to generate a magnetic field that interacts with the body’s hydrogen atoms, producing a signal that is used to reconstruct an image of the body. The sine function’s ability to model the periodic behavior of the magnetic field makes it a critical component in MRI technology.
4. Navigation Systems: GPS and Inertial Navigation

In navigation systems, the sine function is used to describe the motion of objects, such as satellites and vehicles, and to determine their position and velocity. The sine function’s ability to model periodic phenomena makes it an essential tool in understanding the behavior of these systems, allowing for accurate navigation and tracking.
Technical Specifications: GPS
The GPS system uses the sine function to model the motion of satellites and to determine their position and velocity. The sine function’s ability to describe the periodic behavior of the satellites’ orbits makes it a critical component in GPS technology.
5. Music and Acoustics: Sound Waves and Harmonics
In music and acoustics, the sine function is used to model sound waves and harmonics, which are essential components of music and sound. The sine function’s ability to describe periodic phenomena makes it a critical tool in understanding the behavior of sound waves and harmonics, allowing musicians and audio engineers to analyze and manipulate sound for various applications.
What is the sine function used for in physics and engineering?
+The sine function is used to describe the motion of objects, such as pendulums, springs, and vibrating strings, and to analyze and predict their behavior.
How is the sine function used in computer science?
+The sine function is used in signal processing and graphics to generate and manipulate periodic signals and patterns, and to create smooth and realistic animations.
What is the role of the sine function in medical imaging?
+The sine function is used in techniques such as MRI and CT scans to reconstruct images of the body, and to understand the behavior of magnetic fields and X-ray waves.
Meta Description: Discover the five ways the sine function is used in various fields, including physics, engineering, computer science, medical imaging, and navigation systems. Learn how the sine function’s ability to model periodic phenomena makes it a critical component in understanding and analyzing complex systems.



