The Doppler Effect is a fundamental concept in physics that describes the change in frequency or wavelength of a wave in relation to an observer moving relative to the source of the wave. This phenomenon is observed in various forms of waves, including sound waves, light waves, and other types of electromagnetic radiation. The Doppler Effect has numerous applications in fields such as astronomy, radar technology, and medical imaging. In this article, we will delve into the mathematical formulations of the Doppler Effect, exploring five key formulas that underpin our understanding of this phenomenon.
Key Points
- The Doppler Effect is characterized by a change in frequency or wavelength of a wave due to relative motion between the observer and the source.
- The formulas for the Doppler Effect depend on the type of wave and the nature of the motion (longitudinal or transverse).
- For sound waves, the Doppler Effect formula takes into account the velocities of both the source and the observer.
- In the context of light waves, the relativistic Doppler Effect formula incorporates the speed of light and the relative velocity between the source and the observer.
- Understanding and applying these formulas is crucial for calculating the frequency shifts and wavelength changes in various practical scenarios.
Introduction to the Doppler Effect Formulas
The Doppler Effect is a phenomenon that occurs when there is relative motion between the source of a wave and an observer. This relative motion causes a change in the frequency or wavelength of the wave as perceived by the observer. The mathematical formulation of the Doppler Effect varies depending on the type of wave (sound, light, etc.) and the direction of motion (longitudinal or transverse). The following sections will outline five critical formulas related to the Doppler Effect, covering both non-relativistic and relativistic scenarios.
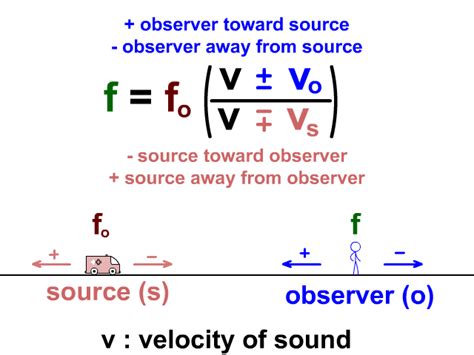
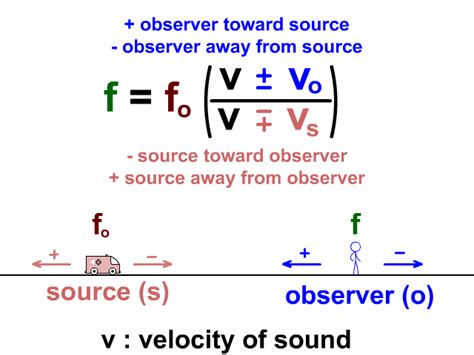
Formula 1: Doppler Effect for Sound Waves
For sound waves, the Doppler Effect formula is given by f’ = f * (v + vo) / (v - vs), where f’ is the observed frequency, f is the emitted frequency, v is the speed of sound, vo is the velocity of the observer, and vs is the velocity of the source. This formula is applicable when both the source and the observer are moving relative to a stationary medium, such as air.
| Variable | Description |
|---|---|
| f' | Observed frequency |
| f | Emitted frequency |
| v | Speed of sound |
| vo | Velocity of the observer |
| vs | Velocity of the source |

Formula 2: Relativistic Doppler Effect for Light Waves
In the context of special relativity, the Doppler Effect for light waves is described by the formula f’ = f * sqrt((1 + v/c) / (1 - v/c)), where c is the speed of light, and v is the relative velocity between the source and the observer. This formula accounts for the relativistic effects that become significant at high speeds, approaching the speed of light.
Formula 3: Transverse Doppler Effect
The transverse Doppler Effect, which occurs when the motion is perpendicular to the direction of wave propagation, is given by f’ = f / gamma, where gamma = 1 / sqrt(1 - v^2/c^2) is the Lorentz factor. This effect is purely relativistic and does not have a non-relativistic counterpart.
Formula 4: Doppler Shift for Radar Technology
In radar applications, the Doppler shift is used to measure the velocity of targets. The formula for the Doppler shift in this context is Δf = (2 * v) / λ, where Δf is the change in frequency, v is the velocity of the target, and λ is the wavelength of the radar wave.
Formula 5: Doppler Effect in Medical Imaging
In medical imaging techniques such as Doppler ultrasound, the formula v = (Δf * c) / (2 * f) is used to calculate the velocity of blood flow or tissue movement, where Δf is the Doppler shift, c is the speed of sound in tissue, and f is the emitted frequency of the ultrasound wave.
What is the primary application of the Doppler Effect in astronomy?
+The primary application is in determining the velocity of celestial objects, such as stars and galaxies, relative to Earth, which is crucial for understanding the expansion of the universe and the motion of celestial bodies.
How does the Doppler Effect affect the perceived pitch of a siren?
+As the siren approaches, the pitch increases due to an increase in frequency, and as it recedes, the pitch decreases due to a decrease in frequency, illustrating the Doppler Effect for sound waves.
What is the significance of the relativistic Doppler Effect in particle physics?
+The relativistic Doppler Effect is crucial for understanding the behavior of high-speed particles and their interactions, which is fundamental in particle physics experiments and theoretical models.
In conclusion, the Doppler Effect is a versatile phenomenon with a wide range of applications, from everyday experiences like the changing pitch of a siren to the sophisticated measurements in astrophysics and particle physics. Understanding the various formulas associated with the Doppler Effect, as outlined in this article, is essential for grasping the underlying physics and for applying these principles in practical scenarios. By integrating these concepts into their work, researchers and practitioners can leverage the Doppler Effect to achieve more accurate measurements, deeper insights, and innovative solutions across multiple disciplines.