The volume flow rate equation is a fundamental concept in physics and engineering, used to calculate the rate at which a fluid flows through a given surface. It is an essential tool in various fields, including fluid dynamics, hydraulics, and chemical engineering. In its simplest form, the volume flow rate equation is expressed as Q = A * v, where Q is the volume flow rate, A is the cross-sectional area of the flow, and v is the average velocity of the fluid.
To understand the volume flow rate equation, it is crucial to grasp the underlying principles of fluid dynamics. The equation is based on the concept of continuity, which states that the mass flow rate of a fluid remains constant throughout a pipe or channel, assuming there are no sources or sinks. The volume flow rate equation is a direct result of this principle, allowing engineers to calculate the rate at which a fluid flows through a given surface.
The volume flow rate equation has numerous applications in various industries. For instance, in chemical engineering, it is used to design and optimize pipelines, pumps, and valves. In civil engineering, it is used to calculate the flow rate of water in rivers, canals, and pipelines. The equation is also essential in the design of hydraulic systems, such as those used in construction equipment and automotive systems.
Key Points
- The volume flow rate equation is expressed as Q = A * v, where Q is the volume flow rate, A is the cross-sectional area, and v is the average velocity.
- The equation is based on the concept of continuity, which states that the mass flow rate of a fluid remains constant throughout a pipe or channel.
- The volume flow rate equation has numerous applications in various industries, including chemical engineering, civil engineering, and hydraulic systems design.
- The equation is essential in calculating the rate at which a fluid flows through a given surface, allowing engineers to design and optimize systems.
- The volume flow rate equation is a fundamental concept in fluid dynamics, and understanding its underlying principles is crucial for accurate calculations and applications.
Derivation of the Volume Flow Rate Equation
The derivation of the volume flow rate equation is based on the concept of continuity, which states that the mass flow rate of a fluid remains constant throughout a pipe or channel. The equation can be derived by considering a small element of fluid moving through a pipe. The mass flow rate of the fluid can be expressed as the product of the density of the fluid, the cross-sectional area of the pipe, and the average velocity of the fluid.
Mathematically, the mass flow rate can be expressed as m = ρ * A * v, where m is the mass flow rate, ρ is the density of the fluid, A is the cross-sectional area, and v is the average velocity. Since the density of the fluid is constant, the mass flow rate can be rewritten as m = ρ * Q, where Q is the volume flow rate. Equating the two expressions for the mass flow rate, we get ρ * Q = ρ * A * v, which simplifies to Q = A * v.
Applications of the Volume Flow Rate Equation
The volume flow rate equation has numerous applications in various industries. In chemical engineering, it is used to design and optimize pipelines, pumps, and valves. The equation is essential in calculating the flow rate of fluids in process plants, allowing engineers to design and optimize systems for maximum efficiency and safety.
In civil engineering, the volume flow rate equation is used to calculate the flow rate of water in rivers, canals, and pipelines. The equation is essential in designing and optimizing hydraulic systems, such as those used in irrigation and water supply systems. The equation is also used in the design of stormwater drainage systems, allowing engineers to calculate the flow rate of water and design systems that can handle heavy rainfall events.
| Application | Industry |
|---|---|
| Pipeline design | Chemical engineering |
| Pump design | Chemical engineering |
| Valve design | Chemical engineering |
| River flow calculation | Civil engineering |
| Canal flow calculation | Civil engineering |
| Pipeline flow calculation | Civil engineering |

Limitations and Assumptions of the Volume Flow Rate Equation

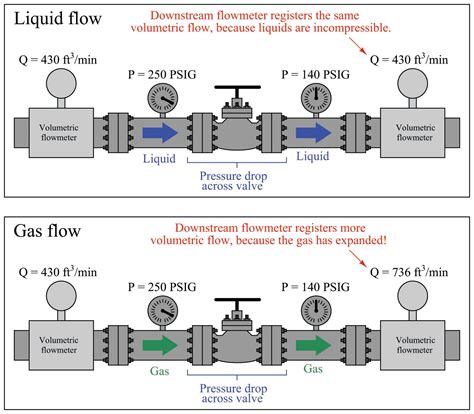
The volume flow rate equation is based on several assumptions and limitations. The equation assumes that the fluid is incompressible, meaning that its density remains constant throughout the flow. The equation also assumes that the flow is steady, meaning that the velocity of the fluid remains constant over time.
In reality, fluids can be compressible, and the flow can be unsteady. The equation can still be applied in these cases, but the results may not be accurate. Additionally, the equation assumes that the flow is one-dimensional, meaning that the velocity of the fluid is constant across the cross-sectional area. In reality, the flow can be multi-dimensional, and the velocity can vary across the cross-sectional area.
Despite these limitations, the volume flow rate equation is a powerful tool in fluid dynamics and engineering. By understanding the underlying principles and assumptions, engineers can apply the equation with confidence, knowing its limitations and potential sources of error.
What is the volume flow rate equation?
+The volume flow rate equation is expressed as Q = A * v, where Q is the volume flow rate, A is the cross-sectional area, and v is the average velocity of the fluid.
What are the assumptions of the volume flow rate equation?
+The volume flow rate equation assumes that the fluid is incompressible, the flow is steady, and the flow is one-dimensional.
What are the limitations of the volume flow rate equation?
+The volume flow rate equation has limitations, including the assumption of incompressibility, steadiness, and one-dimensionality. The equation may not be accurate in cases where these assumptions are not met.
In conclusion, the volume flow rate equation is a fundamental concept in fluid dynamics and engineering. The equation is expressed as Q = A * v, where Q is the volume flow rate, A is the cross-sectional area, and v is the average velocity of the fluid. The equation has numerous applications in various industries, including chemical engineering, civil engineering, and hydraulic systems design. Despite its limitations and assumptions, the equation is a powerful tool in fluid dynamics and engineering, allowing engineers to design and optimize systems for maximum efficiency and safety.